
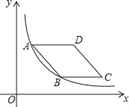
【题目】如图,在平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴平行,A、B两点的纵坐标分别为3,1,反比例函数y=![]() 的图象经过A,B两点,则点D的坐标为( )
的图象经过A,B两点,则点D的坐标为( )
A. (2![]() ﹣1,3)B. (2
﹣1,3)B. (2![]() +1,3)
+1,3)
C. (2![]() ﹣1,3)D. (2
﹣1,3)D. (2![]() +1,3)
+1,3)
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:初中数学 来源: 题型:
【题目】某水果批发商经销一种高档水果,如果每千克盈利5元,每天可售出200千克,经市场调查发现,在进价不变的情况下,若每千克涨价0.1元,销售量将减少1千克
(1)现该商场保证每天盈利1500元,同时又要照顾顾客,那么每千克应涨价多少元?
(2)若该商场单纯从经济利益角度考虑,这种水果每千克涨价多少元,使该商场获利最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABC中,AC=BC,过C作CD//AB.若AD平分∠CAB,则下列说法错误的是( )
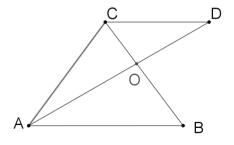
A. BC=CD
B. BO:OC=AB:BC
C. △CDO≌△BAO
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点P从△ABC的顶点B出发,沿B→C→A匀速运动到点A,图2是点P运动时,线段BP的长度y随时间x变化的函数关系图象,其中M为曲线部分的最低点下列说法错误的是( )
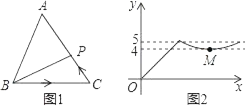
A. △ABC是等腰三角形B. AC边上的高为4
C. △ABC的周长为16D. △ABC的面积为10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.
(1)观察猜想
图1中,线段PM与PN的数量关系是 ,位置关系是 ;
(2)探究证明
把△ADE绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由;
(3)拓展延伸
把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接写出△PMN面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC交AC于点E,AC的反向延长线交⊙O于点F.
(1)试判断直线DE与⊙O的位置关系,并说明理由;
(2)若∠C=30°,⊙O的半径为6,求弓形AF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=2,将线段CD绕点C顺时针旋转90°得到线段CE,线段BD绕点B顺时针旋转90°得到线段BF,连接EF,则图中阴影部分的面积是______.
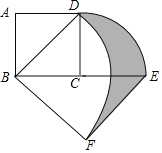
查看答案和解析>>
科目:初中数学 来源: 题型:
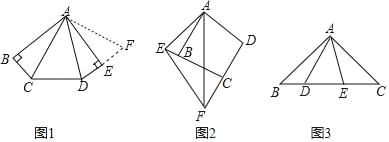
【题目】(1)如图1,在五边形ABCDE中,AB=AE,∠B=∠BAE=∠AED=90°,∠CAD=45°,试猜想BC,CD,DE之间的数量关系.小明经过仔细思考,得到如下解题思路:
将△ABC绕点A逆时针旋转90°至△AEF,由∠B=∠AED=90°,得∠DEF=180°,即点D,E,F三点共线,易证△ACD≌ ,故BC,CD,DE之间的数量关系是 ;
(2)如图2,在四边形ABCD中,AB=AD,∠ABC+∠D=180°,点E,F分别在边CB,DC的延长线上,∠EAF=![]() ∠BAD,连接EF,试猜想EF,BE,DF之间的数量关系,并给出证明.
∠BAD,连接EF,试猜想EF,BE,DF之间的数量关系,并给出证明.
(3)如图3,在△ABC中,∠BAC=90°,AB=AC,点D,E均在边BC上,且∠DAE=45°,若BD=2,CE=3,则DE的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若一次函数y=ax+b和反比例函数y=-![]() 满足a+c=2b,则称为y=ax2+bx+c为一次函数和反比例函数的“等差”函数.
满足a+c=2b,则称为y=ax2+bx+c为一次函数和反比例函数的“等差”函数.
(1)判断y=x+b和y=-![]() 是否存在“等差”函数?若存在,写出它们的“等差”函数;
是否存在“等差”函数?若存在,写出它们的“等差”函数;
(2)若y=5x+b和y=-![]() 存在“等差”函数,且“等差”函数的图象与y=-
存在“等差”函数,且“等差”函数的图象与y=-![]() 的图象的一个交点的横坐标为1,求一次函数和反比例函数的表达式;
的图象的一个交点的横坐标为1,求一次函数和反比例函数的表达式;
(3)若一次函数y=ax+b和反比例函数y=-![]() (其中a>0,c>0,a=
(其中a>0,c>0,a=![]() b)存在“等差”函数,且y=ax+b与“等差”函数有两个交点A(x1,y1)、B(x2,y2),试判断“等差”函数图象上是否存在一点P(x,y)(其中x1<x<x2),使得△ABP的面积最大?若存在,用c表示△ABP的面积的最大值;若不存在,请说明理由.
b)存在“等差”函数,且y=ax+b与“等差”函数有两个交点A(x1,y1)、B(x2,y2),试判断“等差”函数图象上是否存在一点P(x,y)(其中x1<x<x2),使得△ABP的面积最大?若存在,用c表示△ABP的面积的最大值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com