
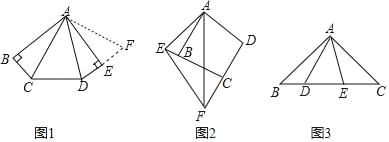
【题目】(1)如图1,在五边形ABCDE中,AB=AE,∠B=∠BAE=∠AED=90°,∠CAD=45°,试猜想BC,CD,DE之间的数量关系.小明经过仔细思考,得到如下解题思路:
将△ABC绕点A逆时针旋转90°至△AEF,由∠B=∠AED=90°,得∠DEF=180°,即点D,E,F三点共线,易证△ACD≌ ,故BC,CD,DE之间的数量关系是 ;
(2)如图2,在四边形ABCD中,AB=AD,∠ABC+∠D=180°,点E,F分别在边CB,DC的延长线上,∠EAF=![]() ∠BAD,连接EF,试猜想EF,BE,DF之间的数量关系,并给出证明.
∠BAD,连接EF,试猜想EF,BE,DF之间的数量关系,并给出证明.
(3)如图3,在△ABC中,∠BAC=90°,AB=AC,点D,E均在边BC上,且∠DAE=45°,若BD=2,CE=3,则DE的长为 .
【答案】(1)△AFD,CD=DE+BC;(2EF=DF﹣BE,理由见解析;(3)![]() .
.
【解析】
(1)如图1,将△ABC绕点A逆时针旋转90°至△AEF,由∠B=∠AED=90°,得∠DEF=180°,即点D,E,F三点共线,易证△ACD≌△AFD,可得结论;
(2)如图2,将△ABE绕点A逆时针旋转,使AB与AD重合,得到△ADE',证明△AFE≌△AFE',据全等三角形的性质解答;
(3)将△ABD绕点A逆时针旋转至△ACD',使AB与AC重合,连接ED',根据全等三角形的性质、勾股定理计算.
(1)BC,CD,DE之间的数量关系为:DF=DE+BC,理由是:
如图1,将△ABC绕点A逆时针旋转90°至△AEF,
由∠B=∠AED=∠AEF=90°,得∠DEF=180°,即点D,E,F三点共线,
∵∠BAE=90°,∠CAD=45°,
∴∠BAC+∠DAE=∠DAE+∠EAF=45°,
∴∠CAD=∠FAD,
∵AD=AD,
∴△ACD≌△FAD(SAS),
∴CD=DF=DE+EF=DE+BC,
故答案为:△AFD,CD=DE+BC;
(2)如图2,EF,BE,DF之间的数量关系是EF=DF﹣BE.
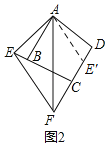
证明:将△ABE绕点A逆时针旋转,使AB与AD重合,得到△ADE',
则△ABE≌△ADE',
∴∠DAE'=∠BAE,AE'=AE,DE'=BE,∠ADE'=∠ABE,
∴∠EAE'=∠BAD,
∵∠ABC+∠ADC=180°,∠ABC+∠ABE=180°,
∠ADE'=∠ADC,即E',D,F三点共线,
又∠EAF=![]() ∠BAD=
∠BAD=![]() ∠EAE'
∠EAE'
∴∠EAF=∠E'AF,
在△AEF和△AE'F中,
 ,
,
∴△AFE≌△AFE'(SAS),
∴FE=FE',
又∵FE'=DF﹣DE',
∴EF=DF﹣BE;
(3)如图3,
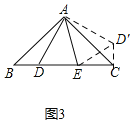
将△ABD绕点A逆时针旋转至△ACD',使AB与AC重合,连接ED',则CD'=BD=2,
由(1)同理得,△AED≌AED',.
∴DE=D'E.
∵∠ACB=∠B=∠ACD'=45°,
∴∠ECD'=90°,
在Rt△ECD'中,ED'=![]() ,即DE=
,即DE=![]() ,
,
故答案为:![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
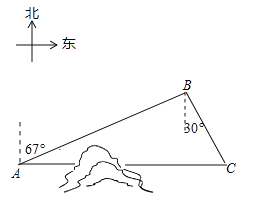
【题目】如图,C地在A地的正东方向,因有大山阻隔,由A地到C地需绕行B地,已知B地位于A地北偏东67°方向,距离A地520km,C地位于B地南偏东30°方向,若打通穿山隧道,建成两地直达高铁,求A地到C地之间高铁线路的长.(结果保留整数)
(参考数据:sin67°≈![]() ,cos67°≈
,cos67°≈![]() ,tan67°≈
,tan67°≈![]() ,
,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
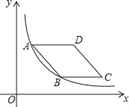
【题目】如图,在平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴平行,A、B两点的纵坐标分别为3,1,反比例函数y=![]() 的图象经过A,B两点,则点D的坐标为( )
的图象经过A,B两点,则点D的坐标为( )
A. (2![]() ﹣1,3)B. (2
﹣1,3)B. (2![]() +1,3)
+1,3)
C. (2![]() ﹣1,3)D. (2
﹣1,3)D. (2![]() +1,3)
+1,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
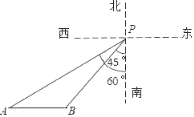
【题目】在某海域,一艘海监船在P处检测到南偏西45°方向的B处有一艘不明船只,正沿正西方向航行,海监船立即沿南偏西60°方向以40海里/小时的速度去截获不明船只,经过1.5小时,刚好在A处截获不明船只,求不明船只的航行速度.(![]() ≈1.41,
≈1.41,![]() ≈1.73,结果保留一位小数).
≈1.73,结果保留一位小数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育用品商店用4000元购进一批足球,全部售完后,又用3600元再次购进同样的足球,但这次每个足球的进价是第一次进价的1.2倍,且数量比第一次少了10个.
(1)求第一次每个足球的进价是多少元?
(2)若第二次进货后按150元/个的价格销售,当售出10个后,根据市场情况,商店决定对剩余的足球全部按同一标准一次性打折售完,但要求这次的利润不少于450元,问该商店最低可打几折销售?
查看答案和解析>>
科目:初中数学 来源: 题型:
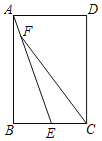
【题目】如图,在矩形ABCD中,点E是BC上一点,连接AE,点F是AE上一点,连接FC,若∠BAE=∠EFC,CF=CD,AB:BC=3:2,AF=4,则FC的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
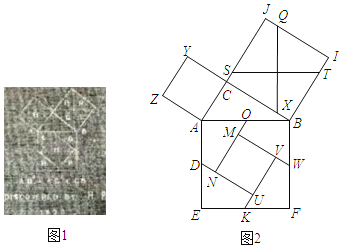
【题目】勾股定理有着悠久的历史,它曾引起很多人的兴趣.英国佩里加(H.Perigal,1801﹣1898)用“水车翼轮法”(图1)证明了勾股定理.该证法是用线段QX,ST,将正方形BIJC分割成四个全等的四边形,再将这四个四边形和正方形ACYZ拼成大正方形AEFB(图2).若AD=![]() ,tan∠AON=
,tan∠AON=![]() ,则正方形MNUV的周长为( )
,则正方形MNUV的周长为( )
A. ![]() B. 18C. 16D.
B. 18C. 16D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
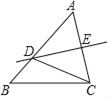
【题目】如图,在△ABC中,AB=5,AC=4,∠A=60°,若边AC的垂直平分线DE交AB于点D,连接CD,则△BDC的周长为( )
A. 8 B. 9 C. 5+![]() D. 5+
D. 5+![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com