
【题目】某体育用品商店用4000元购进一批足球,全部售完后,又用3600元再次购进同样的足球,但这次每个足球的进价是第一次进价的1.2倍,且数量比第一次少了10个.
(1)求第一次每个足球的进价是多少元?
(2)若第二次进货后按150元/个的价格销售,当售出10个后,根据市场情况,商店决定对剩余的足球全部按同一标准一次性打折售完,但要求这次的利润不少于450元,问该商店最低可打几折销售?
【答案】(1)100元;(2) 7.5折
【解析】
(1)设第一次每个足球的进价是x元,则第二次每个足球的进价是1.2x元,根据数量关系:第一次购进足球的数量﹣10个=第二次购进足球的数量,可得分式方程,然后求解即可;
(2)设商店对剩余的足球按同一标准一次性打a折销售时,可使利润不少于450元.先根据(1)中求得的数得到第二次购进足球的数量和价格,再根据数量关系:第一次销售完10个获得的利润+第二次打折销售完足球获得的利润≥450元,列出不等式,然后求解即可得出答案.
(1)设第一次每个足球的进价是x元,则第二次每个足球的进价是1.2x元,
根据题意得,![]() =10,
=10,
解得:x=100,
经检验:x=100是原方程的根,
答:第一次每个足球的进价是100元;
(2)设该商店最低可打a折销售,
根据题意得,150×10+(![]() ﹣10)×150×
﹣10)×150×![]() ﹣3600≥450,
﹣3600≥450,
解得:a=7.5
答:该商店最低可打7.5折销售.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于A (-1,0),B (5,0)两点,直线
轴交于A (-1,0),B (5,0)两点,直线![]() 与y轴交于点
与y轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .点
.点![]() 是x轴上方的抛物线上一动点,过点
是x轴上方的抛物线上一动点,过点![]() 作
作![]() ⊥
⊥![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() .
.
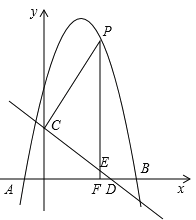
(1)求抛物线的解析式;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)若点![]() 是点
是点![]() 关于直线
关于直线![]() 的对称点,是否存在点
的对称点,是否存在点![]() ,使点
,使点![]() 落在
落在![]() 轴上?若存在,请直接写出相应的点
轴上?若存在,请直接写出相应的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.
(1)观察猜想
图1中,线段PM与PN的数量关系是 ,位置关系是 ;
(2)探究证明
把△ADE绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由;
(3)拓展延伸
把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接写出△PMN面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=2,将线段CD绕点C顺时针旋转90°得到线段CE,线段BD绕点B顺时针旋转90°得到线段BF,连接EF,则图中阴影部分的面积是______.
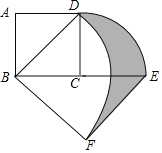
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.
(1)求证:四边形EFDG是菱形;
(2)求证:EG2=![]() GF
GF![]() AF;
AF;
(3)若AB=4,BC=5,求GF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在五边形ABCDE中,AB=AE,∠B=∠BAE=∠AED=90°,∠CAD=45°,试猜想BC,CD,DE之间的数量关系.小明经过仔细思考,得到如下解题思路:
将△ABC绕点A逆时针旋转90°至△AEF,由∠B=∠AED=90°,得∠DEF=180°,即点D,E,F三点共线,易证△ACD≌ ,故BC,CD,DE之间的数量关系是 ;
(2)如图2,在四边形ABCD中,AB=AD,∠ABC+∠D=180°,点E,F分别在边CB,DC的延长线上,∠EAF=![]() ∠BAD,连接EF,试猜想EF,BE,DF之间的数量关系,并给出证明.
∠BAD,连接EF,试猜想EF,BE,DF之间的数量关系,并给出证明.
(3)如图3,在△ABC中,∠BAC=90°,AB=AC,点D,E均在边BC上,且∠DAE=45°,若BD=2,CE=3,则DE的长为 .
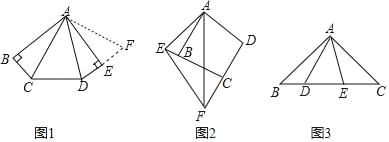
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市卫生局为了了解该市社区医院对患者随访情况,随机抽查了部分社区医院一年来对患者随访的次数,并用得到的数据绘制了两幅统计图,下面给出了两幅不完整的统计图:
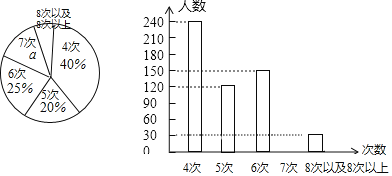
请根据图中提供的信息,回答下列问题:
(1)该市卫生局共抽查了社区医院的患者多少人?并补全条形统计图;
(2)请直接写出在这次抽样调查中的众数是 ,中位数是 ;
(3)如果该市社区医院患者有60000人,请你估计“随访的次数不少于7次”社区医院的患者有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,某超市从一楼到二楼有一自动扶梯,图2是侧面示意图.已知自动扶梯AB的坡度为1:2.4,AB的长度是13米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处测得C点的仰角为42°,求二楼的层高BC约为多少米?( sin42°≈0.7,tan42°≈0.9)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着生活水平的提高,人们对空气质量的要求也越来越高,为了了解3月中旬长春市城区的空气质量情况,某校“综合实践环境调查小组”,从“2345天气预报”网,抽取了朝阳区和南关区这两个城区2019年3月11日﹣2019年3月20日的空气质量指数,作为样本进行统计,过程如下,请补充完整收集数据
朝阳区 | 167 | 61 | 79 | 78 | 97 | 153 | 59 | 179 | 85 | 209 |
南关区 | 74 | 54 | 47 | 47 | 43 | 43 | 59 | 104 | 119 | 251 |
(备注:空气质量指数,简称AQI,是定期描述空气质量的)
整理、描述数据按下表整理,描述这两城区空气质量指数的数据:
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 |
朝阳区 |
|
|
|
|
|
南关区 | 4 | 3 | 2 | 0 | 1 |
(说明:空气质量指数≤50时,空气质量为优,50<空气质量指数≤100时,空气场量为良,100<空气质量指数≤150时,空气质量为轻微污染,150<空气质量指数≤200时,空气质量为中度污染,200<空气质量指数≤300时,空气质量为重度污染)
分析数据
两城区的空气质量指数的平均数、中位数、方差如下表所示
城区 | 平均数 | 中位数 | 方差 |
朝阳区 | 116.7 | 91 | 2999.12 |
南关区 | 84.1 |
| 4137.66 |
请将以上两个表格补充完整得出结论
可以推断出哪个城区这十天中空气质量情况比较好?请至少从两个不同的角度说明推断的合理性
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com