
°Њћвƒњ°њ»зЌЉ£ђ‘Џ∆љ√ж÷±љ«„ш±кѕµ÷–£ђ≈„ќпѕя![]() љї
љї![]() ÷б”Џ
÷б”Џ![]() £ђ
£ђ![]() Ѕљµг£®µг
Ѕљµг£®µг![]() ‘Џµг
‘Џµг![]() µƒ„у±я£©љї
µƒ„у±я£©љї![]() ÷б’э∞л÷б”Џµг
÷б’э∞л÷б”Џµг![]() £ђµг
£ђµг![]() ќ™≈„ќпѕяґ•µг.
ќ™≈„ќпѕяґ•µг.
£®1£©÷±љ”–і≥ц![]() »эµгµƒ„ш±кЉ∞
»эµгµƒ„ш±кЉ∞![]() µƒ÷µ£ї
µƒ÷µ£ї
£®2£©µг![]() ќ™≈„ќпѕя‘Џ
ќ™≈„ќпѕя‘Џ![]() ÷б…ѕЈљµƒ“їµг£ђ«“
÷б…ѕЈљµƒ“їµг£ђ«“![]() £ђ«уµг
£ђ«уµг![]() µƒ„ш±к£ї
µƒ„ш±к£ї
£®3£©‘Џ£®2£©µƒћхЉюѕ¬£ђ![]() ќ™
ќ™![]() µƒЌв–ƒ£ђµг
µƒЌв–ƒ£ђµг![]() £ђµг
£ђµг![]() Ј÷±рі”µг
Ј÷±рі”µг![]() Ќђ ±≥цЈҐ“‘2µ•ќї/
Ќђ ±≥цЈҐ“‘2µ•ќї/![]() £ђ1µ•ќї/
£ђ1µ•ќї/![]() Ћўґ»—Ў…дѕя
Ћўґ»—Ў…дѕя![]() £ђ
£ђ![]() „ч‘»Ћў‘Ћґѓ£ђ‘Ћґѓ ±Љдќ™
„ч‘»Ћў‘Ћґѓ£ђ‘Ћґѓ ±Љдќ™![]() √л£®
√л£®![]() «“
«“![]() £©£ђ÷±ѕя
£©£ђ÷±ѕя![]() љї”Џ
љї”Џ![]() .
.
Ґў«у÷§£Їµг![]() ‘Џґ®÷±ѕя
‘Џґ®÷±ѕя![]() …ѕ≤Ґ«у
…ѕ≤Ґ«у![]() µƒљвќц љ£ї
µƒљвќц љ£ї
ҐЏ»ф![]() ‘Џ≈„ќпѕя…ѕ«“‘Џ÷±ѕя
‘Џ≈„ќпѕя…ѕ«“‘Џ÷±ѕя![]() ѕ¬Јљ£ђµ±
ѕ¬Јљ£ђµ±![]() µљ÷±ѕя
µљ÷±ѕя![]() Њајл„оіу ±£ђ«уµг
Њајл„оіу ±£ђ«уµг![]() µƒ„ш±к.
µƒ„ш±к.
°Њір∞Є°њ£®1£©![]() £ї£®2£©
£ї£®2£©![]() £ї£®3£©Ґў
£ї£®3£©Ґў![]() £ђЉыљвќц£ђҐЏ
£ђЉыљвќц£ђҐЏ![]()
°Њљвќц°њ
£®1£©љЂy=0£ђx=0іъ»лЉіњ…–і≥ц![]() »эµгµƒ„ш±кЉ∞
»эµгµƒ„ш±кЉ∞![]() µƒ÷µ£ї
µƒ÷µ£ї
£®2£©ѕ»«у![]() µƒљвќц љќ™
µƒљвќц љќ™![]() £ђЅ™ЅҐ
£ђЅ™ЅҐ![]() љвµ√£Ї
љвµ√£Ї![]() £®…б»•£©£ђ
£®…б»•£©£ђ![]() £ђњ…µ√
£ђњ…µ√![]() .
.
£®3£©Ґў…и![]() £ђ‘т
£ђ‘т![]() £ђњ…
£ђњ…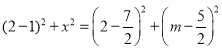 љвµ√£Ї
љвµ√£Ї![]() £ђ
£ђ![]() £ђ…и
£ђ…и![]() £ђ‘т
£ђ‘т![]() £ђµ±
£ђµ±![]() ±£ђ
±£ђ![]() њ…µ√
њ…µ√![]() µ±
µ±![]() ±£ђЌђјнњ…«у
±£ђЌђјнњ…«у![]() £ђє
£ђє ![]() ‘Џ÷±ѕя
‘Џ÷±ѕя![]() …ѕ.
…ѕ.
ҐЏµ±![]() µљ
µљ![]() Њајл„оіу ±£ђ…иєэ
Њајл„оіу ±£ђ…иєэ![]() «“”л
«“”л![]() ∆љ––µƒ÷±ѕяµƒљвќц љќ™£Ї
∆љ––µƒ÷±ѕяµƒљвќц љќ™£Ї ![]() Ѕ™ЅҐ
Ѕ™ЅҐ![]() јы”√Є√Јљ≥ћ„й”–ЅљЄцѕаµ»µƒ µ эЄщ£ђњ…µ√Јљ≥ћ
јы”√Є√Јљ≥ћ„й”–ЅљЄцѕаµ»µƒ µ эЄщ£ђњ…µ√Јљ≥ћ![]() ”–ЅљЄцѕаµ»µƒ µ эЄщ£ђ«уµ√
”–ЅљЄцѕаµ»µƒ µ эЄщ£ђ«уµ√![]() £ђє
£ђє ![]() £ђњ…µ√µг
£ђњ…µ√µг![]() µƒ„ш±к.
µƒ„ш±к.
£®1£©°я≈„ќпѕя![]() £ђµг
£ђµг![]() ќ™≈„ќпѕяґ•µг.
ќ™≈„ќпѕяґ•µг.
°а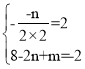
љвµ√![]()
°а![]()
µ±y=0 ±£ђ![]()
љвµ√![]()
°а![]()
µ±x=0 ±£ђ![]()
љвµ√![]()
°а![]()
°а![]()
£®2£©°я![]()
°а![]()
…и![]() µƒљвќц љќ™
µƒљвќц љќ™![]()
”÷“тќ™A£®1£ђ0£©.іъ»л![]() љвµ√£Їb=-1
љвµ√£Їb=-1
є ![]() µƒљвќц љќ™
µƒљвќц љќ™![]() £ђ
£ђ
°а![]()
љвµ√£Ї![]() £®…б»•£©£ђ
£®…б»•£©£ђ![]() £ђ
£ђ
°а![]() .
.
£®3£©Ґў…и![]() £ђ
£ђ![]() £ђ
£ђ
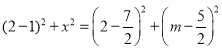
љвµ√£Ї![]() £ђ
£ђ![]() £ђ
£ђ
…и![]() £ђ
£ђ![]() £ђ
£ђ
µ±![]() ±£ђ
±£ђ![]()
µ±![]() ±£ђЌђјнњ…«у
±£ђЌђјнњ…«у![]() £ђє
£ђє ![]() ‘Џ÷±ѕя
‘Џ÷±ѕя![]() …ѕ.
…ѕ.
ҐЏµ±![]() µљ
µљ![]() Њајл„оіу ±£ђ…иєэ
Њајл„оіу ±£ђ…иєэ![]() «“”л
«“”л![]() ∆љ––µƒ÷±ѕяµƒљвќц љќ™£Ї
∆љ––µƒ÷±ѕяµƒљвќц љќ™£Ї
![]()
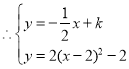 ”–Ѕљµ»Єщ
”–Ѕљµ»Єщ
![]() ”–µ»Єщ£ђ
”–µ»Єщ£ђ![]()
![]()


 «б«…ґбєЏ÷№≤⑬њЉ÷±Ќ®÷–њЉѕµЅ–ір∞Є
«б«…ґбєЏ÷№≤⑬њЉ÷±Ќ®÷–њЉѕµЅ–ір∞Є
| ƒкЉґ | Єя÷–њќ≥ћ | ƒкЉґ | ≥х÷–њќ≥ћ |
| Єя“ї | Єя“ї√вЈ—њќ≥ћЌ∆Љц£° | ≥х“ї | ≥х“ї√вЈ—њќ≥ћЌ∆Љц£° |
| Єяґю | Єяґю√вЈ—њќ≥ћЌ∆Љц£° | ≥хґю | ≥хґю√вЈ—њќ≥ћЌ∆Љц£° |
| Єя»э | Єя»э√вЈ—њќ≥ћЌ∆Љц£° | ≥х»э | ≥х»э√вЈ—њќ≥ћЌ∆Љц£° |
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
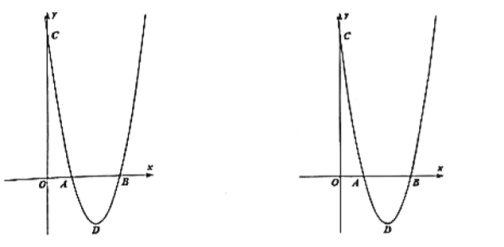
°Њћвƒњ°њ»зЌЉ£ђ“їіќЇѓ эy£љkx+b£®k°Ґbќ™≥£ э£ђk°ў0£©µƒЌЉѕу”лx÷б°Ґy÷бЈ÷±рљї”ЏA°ҐBЅљµг£ђ«“”лЈі±»јэЇѓ эy£љ![]() £®mќ™≥£ э«“m°ў0£©µƒЌЉѕу‘ЏµЏґюѕуѕёљї”ЏµгC£ђCD°Ќx÷б£ђіє„гќ™D£ђ»фOB£љ2OA£љ3OD£љ6£Ѓ
£®mќ™≥£ э«“m°ў0£©µƒЌЉѕу‘ЏµЏґюѕуѕёљї”ЏµгC£ђCD°Ќx÷б£ђіє„гќ™D£ђ»фOB£љ2OA£љ3OD£љ6£Ѓ
£®1£©«у“їіќЇѓ э”лЈі±»јэЇѓ эµƒљвќц љ£ї
£®2£©«уЅљЄцЇѓ эЌЉѕуµƒЅн“їЄцљїµгEµƒ„ш±к£ї
£®3£©«лєџ≤мЌЉѕу£ђ÷±љ”–і≥ц≤їµ» љkx+b°Ё![]() µƒљвЉѓ£Ѓ
µƒљвЉѓ£Ѓ
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
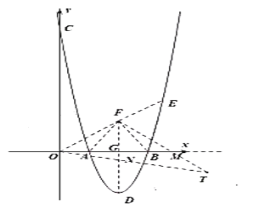
°Њћвƒњ°њ»зЌЉ£ђґюіќЇѓ э![]() µƒЌЉѕу”лx÷бљї”ЏA£ђBЅљµг£ђ”лy÷бљї”ЏµгC£ђґ‘≥∆÷б”лx÷бљї”ЏµгD£ђ»фµгPќ™y÷б…ѕµƒ“їЄцґѓµг£ђЅђљ”PD£ђ‘т
µƒЌЉѕу”лx÷бљї”ЏA£ђBЅљµг£ђ”лy÷бљї”ЏµгC£ђґ‘≥∆÷б”лx÷бљї”ЏµгD£ђ»фµгPќ™y÷б…ѕµƒ“їЄцґѓµг£ђЅђљ”PD£ђ‘т![]() µƒ„о–°÷µќ™________.
µƒ„о–°÷µќ™________.
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
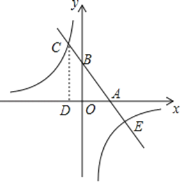
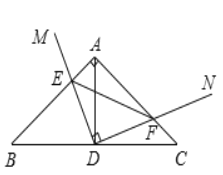
°Њћвƒњ°њ»зЌЉ£ђ‘Џ![]() ÷–£ђ
÷–£ђ![]() £ђµг
£ђµг![]() ќ™
ќ™![]() µƒ÷–µг£ђ
µƒ÷–µг£ђ![]() £ђ
£ђ![]() »∆µг
»∆µг![]() –э„™£ђ
–э„™£ђ![]() °Ґ
°Ґ![]() Ј÷±р”л±я
Ј÷±р”л±я![]() °Ґ
°Ґ![]() љї”Џ°Ґ
љї”Џ°Ґ![]() Ѕљµг.ѕ¬Ѕ–љб¬џ£ЇҐў
Ѕљµг.ѕ¬Ѕ–љб¬џ£ЇҐў![]() £їҐЏ
£їҐЏ![]() £їҐџ
£їҐџ![]() £їҐ№
£їҐ№![]() £їҐЁ
£їҐЁ![]() ”л
”л![]() њ…ƒ№ї•ѕа∆љЈ÷.
њ…ƒ№ї•ѕа∆љЈ÷.
∆д÷–£ђ’э»Јµƒљб¬џ «___________________£®ћо–тЇ≈£©
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
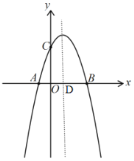
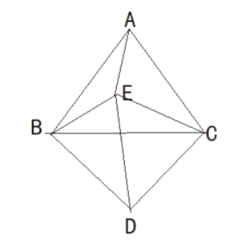
°Њћвƒњ°њ»зЌЉ£ђ“—÷™![]() ЇЌ
ЇЌ![]() ґЉќ™µ»±я»эљ«–ќ£ђ‘т
ґЉќ™µ»±я»эљ«–ќ£ђ‘т![]() ”л
”л![]() µƒ эЅњєЎѕµ’э»Јµƒ «£® £©
µƒ эЅњєЎѕµ’э»Јµƒ «£® £©
A.![]() B.
B.![]()
C.![]() D.
D.![]()
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ»зЌЉ£ђ‘ЏRt°чABC÷–£ђ°ѕC=90°г£ђAC=8£ђsin A=![]()
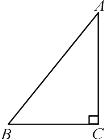
(1)«уABµƒ≥§;
(2)»фµгE‘ЏRt°чABCµƒ÷±љ«±я…ѕ£ђµгF‘Џ–±±яAB…ѕ£ђµ±°чCFE°„°чABC ±£ђ«уCEµƒ≥§.
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ»зЌЉ1£ђ≥§Јљ–ќABCD÷–£ђ°ѕDAB£љ°ѕB£љ°ѕDCB£љ°ѕD£љ90°г£ђAD£љBC£љ6£ђAB£љCD£љ10£ЃµгEќ™…дѕяDC…ѕµƒ“їЄцґѓµг£ђ∞—°чADE—Ў÷±ѕяAEЈ≠’џµ√°чAD°дE£Ѓ
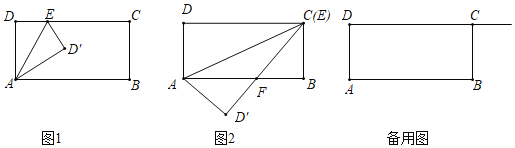
£®1£©µ±D°дµг¬д‘ЏAB±я…ѕ ±£ђ°ѕDAE£љ°° °°°г£ї
£®2£©»зЌЉ2£ђµ±Eµг”лCµг÷ЎЇѕ ±£ђD°дC”лABљїµгF£ђ
Ґў«у÷§£ЇAF£љFC£їҐЏ«уAF≥§£Ѓ
£®3£©Ѕђљ”D°дB£ђµ±°ѕAD°дB£љ90°г ±£ђ«уDEµƒ≥§£Ѓ
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њєЎ”Џµƒ“ї‘™ґюіќЈљ≥ћx2+2x+k+1=0µƒ µ эљв «x1ЇЌx2£Ѓ
£®1£©«уkµƒ»°÷µЈґќІ£ї
£®2£©»зєыx1+x2©Бx1x2£Љ©Б1«“kќ™’ы э£ђ«уkµƒ÷µ£Ѓ
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њƒ≥ЌжЊя≈ъЈҐ…ћѕъ џ√њЉюљшЉџќ™40‘™µƒЌжЊя£ђ –≥°µч≤йЈҐѕ÷£ђ»ф“‘√њЉю50‘™µƒЉџЄсѕъ џ£ђ∆љЊщ√њћмѕъ џ90Љю£ђµ•Љџ√њћбЄя1‘™£ђ∆љЊщ√њћмЊЌ…ўѕъ џ3Љю£Ѓ
(1)∆љЊщ√њћмµƒѕъ џЅњy(Љю)”лѕъ џЉџx(‘™/Љю)÷ЃЉдµƒЇѓ эєЎѕµ љќ™°° °°£ї
(2)«уЄ√≈ъЈҐ…ћ∆љЊщ√њћмµƒѕъ џјы»уW(‘™)”лѕъ џЉџx(‘™/Љю)÷ЃЉдµƒЇѓ эєЎѕµ љ£ї
(3)ќпЉџ≤њ√≈єжґ®√њЉю џЉџ≤їµ√Єя”Џ55‘™£ђµ±√њЉюЌжЊяµƒѕъ џЉџќ™ґа…ў‘™ ±£ђњ…“‘їсµ√„оіујы»у£њ„оіујы»у «ґа…ў‘™£њ
≤йњіір∞ЄЇЌљвќц>>
єъЉ —І–£”≈—° - ЅЈѕ∞≤бЅ–±н - ‘ћвЅ–±н
Їю±± °ї•Ѕ™Ќшќ•Ј®ЇЌ≤їЅЉ–≈ѕҐЊў±®∆љћ® | Ќш…ѕ”–Ї¶–≈ѕҐЊў±®„®«ш | µз–≈’©∆≠Њў±®„®«ш | …жјъ Ј–йќё÷ч“е”–Ї¶–≈ѕҐЊў±®„®«ш | …ж∆у«÷»®Њў±®„®«ш
ќ•Ј®ЇЌ≤їЅЉ–≈ѕҐЊў±®µзї∞£Ї027-86699610 Њў±®” ѕд£Ї58377363@163.com