【题目】已知函数
与
轴交与
，
两点，与
轴交与
点，则能使
是直角三角形的抛物线条数是（ ）
A. 0 B. 1 C. 2 D. 3
【答案】B
【解析】
首先求出抛物线与坐标轴的交点坐标，然后利用勾股定理求出AB和BC的长，再次根据△ABC是直角三角形，利用勾股定理列出n的一元二次方程，求出n的值即可．
令y=（x﹣n）（x﹣3）=0，解得：x=n或x=3．
假设3＞n，A（3，0），B（n，0），令x=0，y=3n，即C点坐标为（0，3n），根据图形知：CB2=9+9n2，AC2=n2+9n2，AB2=（3﹣n）2，根据题意知△ABC是直角三角形，即BC2+AC2=AB2，整理得：9+9n2+n2+9n2=9﹣6n+n2，18n2+6n=0，解得：n=0或n=﹣
．
当n=0时，这样的抛物线不满足题意，即n=﹣，所以能使△ABC是直角三角形的抛物线条数是1条．
故选B．
科目：初中数学 来源： 题型：
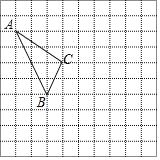
【题目】在如图所示的正方形网格中，每个小正方形的边长为1，格点三角形（顶点是网格线的交点的三角形）ABC的顶点A，C的坐标分别为（﹣4，5），（﹣1，3）．
（1）请在如图所示的网格平面内作出平面直角坐标系；并写出B点坐标；
（2）请作出△ABC关于y轴对称的△A'B'C'；
（3）请作出将△ABC向下平移的3个单位，再向右平移5个单位后的△A1B1C1；则点A1的坐标为_____；点B1的坐标为______，
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，剪两张对边平行且宽度相等的纸条随意交叉叠放在一起，转动其中一张，重合部分构成一个四边形，则下列结论中不一定成立的是（ ）
A. ∠ABC=∠ADC，∠BAD=∠BCD B. AB=BC
C. AB=CD，AD=BC D. ∠DAB+∠BCD=180°
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小迪同学在学勾股定理时发现一类特殊三角形：在一个三角形中，如果一个角是另一个角的2倍，那么称这个三角形为“倍角三角形”.
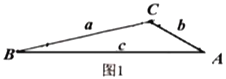
如图1，在倍角
中，
，
、
、
的对边分别记为
，
，
，三角形的三边，，有什么关系呢？让我们一起来探索……
（1）已知“倍角三角形”的一个内角为
，则这个三角形的另两个角的度数分别为______
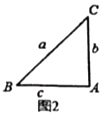
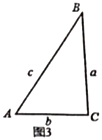
（2）小迪同学先从特殊的“倍角三角形”入手研究，请你结合图2和图3填写下表：
三角形 | 角的已知量 |
|
|
图2 |
| ______ | ______ |
图3 |
| ______ |
小迪同学根据上表，提出一般性猜想：在“倍角三角形”中，，那么，，三边满足：______；
（3）如图1：在倍角三角形中，
，、、的对边分别记为，，，求证：
.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，
中，
，已知
，
与
相交于点
，
与相交于点
，
与相交于点
.
（1）如图，观察并猜想
和
有怎样的数量关系？并说明理由.
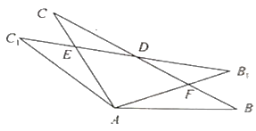
（2）筝形的定义：两组邻边分别相等的四边形叫做筝形. 如上图，证明四边形
是筝形.
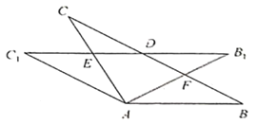
（3）如图，若
，其他条件不变，求
的长度.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在△ABC中，AB=AC，∠BAC=
（
），将线段BC绕点B逆时针旋转60°得到线段BD。
（1）如图1，直接写出∠ABD的大小（用含的式子表示）；
（2）如图2，∠BCE=150°，∠ABE=60°，判断△ABE的形状并加以证明；
（3）在（2）的条件下，连结DE，若∠DEC=45°，求
的值。
查看答案和解析>>
科目：初中数学 来源： 题型：
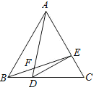
【题目】如图，
是等边三角形，点
、
分别在
、
上，且
，
，
、
相交于点
，连接
，则下列结论：①
；②
；③
；④
，正确的结论有（ ）
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
