
����Ŀ��С��ͬѧ��ѧ���ɶ���ʱ����һ�����������Σ���һ���������У����һ��������һ���ǵ�2������ô�����������Ϊ��������������.
��ͼ1���ڱ���![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() �ĶԱ߷ֱ��Ϊ
�ĶԱ߷ֱ��Ϊ![]() ��
��![]() ��
��![]() �����������
�����������![]() ��
��![]() ��
��![]() ��ʲô��ϵ�أ�������һ����̽������
��ʲô��ϵ�أ�������һ����̽������
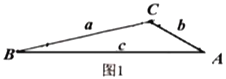
��1����֪����������������һ���ڽ�Ϊ![]() ������������ε��������ǵĶ����ֱ�Ϊ______
������������ε��������ǵĶ����ֱ�Ϊ______
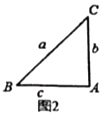
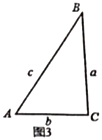
��2��С��ͬѧ�ȴ�������������������������о���������ͼ2��ͼ3��д�±���
������ | �ǵ���֪�� |
|
|
ͼ2 |
| ______ | ______ |
ͼ3 |
| ______ |
С��ͬѧ�����ϱ������һ���Բ��룺�����������������У�![]() ����ô
����ô![]() ��
��![]() ��
��![]() �������㣺______��
�������㣺______��
��3����ͼ1���ڱ����������У�![]() ��
��![]() ��
��![]() ��
��![]() �ĶԱ߷ֱ��Ϊ
�ĶԱ߷ֱ��Ϊ![]() ��
��![]() ��
��![]() ����֤��
����֤��![]() .
.
���𰸡���1��10�㣻20�㣻��2��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ����3��������.
����3��������.
��������
��1�����������ڽǺͣ����ɵý⣻
��2��ͼ2�������Σ���Ȼ�ǵ���ֱ�������Σ�����б��![]() Ϊ2����ô
Ϊ2����ô![]() ���������
���������![]() ��
��![]() ��ֵ��ͼ3�Ľⷨͬ�ϣ�
��ֵ��ͼ3�Ľⷨͬ�ϣ�
��3���ɣ�2���н��ۣ����μ��ɵ�֤.
��1�������⣬�����������ڽǺ�Ϊ180��-150��=30��
�ɱ��ǹ�ϵ�������������ڽǵĶ����ֱ�Ϊ10�㡢20�㣻
��2����б��Ϊ2��
��![]() ʱ����ô
ʱ����ô![]() ��
��
��![]()
��![]() ʱ��
ʱ��![]()
��![]()
![]() ��
��![]() ��
��![]() �������㣺
�������㣺![]() ��
��
��3���ɣ�2���н��ۣ���
![]()
��![]()
���ɵ�֤.


 ��ĩ1�����ʽ���������ϵ�д�
��ĩ1�����ʽ���������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
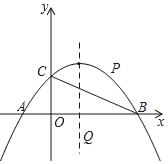
����Ŀ����ͼ����֪��A����1��0����B��3��0����C��0��1����������y=ax2+bx+c�ϣ�
��1���������߽���ʽ��
��2����ֱ��BC�Ϸ�������������һ��P��ʹ��PBC���Ϊ1��
��3����x���·����������߶Գ����ϣ��Ƿ����һ��Q��ʹ��BQC=��BAC�������ڣ����Q�����ꣻ�������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() .
.
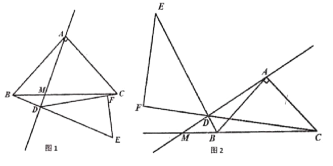
��1����ͼ1����ֱ��![]() ��
��![]() �ཻ��
�ཻ��![]() ������
������![]() ��
��![]() ��
��![]() ������
������![]() ���ӳ�
���ӳ�![]() ��
��![]() ��ʹ��
��ʹ��![]() ������
������![]() ��
��![]() ��
��![]() ��֤����
��֤����![]() .
.
��2����ͼ2����ֱ��![]() ��
��![]() ���ӳ����ཻ��
���ӳ����ཻ��![]() ������
������![]() ��
��![]() ��
��![]() ������
������![]() ���ӳ�
���ӳ�![]() ��
��![]() ��ʹ��
��ʹ��![]() ������
������![]() ��
��![]() ��
��![]() ���ӳ�����
���ӳ�����![]() ��̽����
��̽����![]() ��
��![]() ��
��![]() ֮���������ϵ����֤��.
֮���������ϵ����֤��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
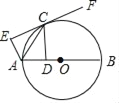
����Ŀ����ͼ��AB����O��ֱ������CΪ��O��һ�㣬����C��CD��AB�ڵ�D��CF����O�����ߣ�����A��AE��CF��E������AC��
��1����֤��AE=AD��
��2����AE=3��CD=4����AB�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ĸ���״��С��ͬ�ĵ��������ΰ���ͼ��ʾ��ʽ�ڷţ���֪![]() ��
��![]() ������
������![]() ����
����![]() ���ӳ����ϣ���ͼ����Ӱ���ֵ����Ϊ�� ��
���ӳ����ϣ���ͼ����Ӱ���ֵ����Ϊ�� ��

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ͼ��![]() ��Բ
��Բ![]() ֱ����
ֱ����![]() ��Բ
��Բ![]() �����ߣ��е�Ϊ
�����ߣ��е�Ϊ![]() ��
��![]() ƽ������
ƽ������![]() ��
��![]() ��
��![]() ���ӳ��߽��ڵ�
���ӳ��߽��ڵ�![]() ����
����![]() ����
����![]() ��
��![]() �ij��ǹ���
�ij��ǹ���![]() �ķ���
�ķ���![]() ��������
��������

![]() ֤����
֤����![]() ��Բ
��Բ![]() �����ߣ�
�����ߣ�
![]() ���߶�
���߶�![]() �ij���
�ij���
![]() ��
��![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() �ύ��
�ύ��![]() ��
��![]() ���㣬��
���㣬��![]() �ύ��
�ύ��![]() �㣬����ʹ
�㣬����ʹ![]() ��ֱ�������ε������������ǣ� ��
��ֱ�������ε������������ǣ� ��
A. 0 B. 1 C. 2 D. 3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ����У���ƻ������Ϊ![]() ����������̻������żס����������̶����.��֪��ÿ��������̻���������Ҷ�ÿ��������̻��������2���������ڶ���������Ϊ
����������̻������żס����������̶����.��֪��ÿ��������̻���������Ҷ�ÿ��������̻��������2���������ڶ���������Ϊ![]() ������̻�ʱ���ӱ��Ҷ�����4�졣
������̻�ʱ���ӱ��Ҷ�����4�졣
��1����ס��������̶�ÿ��������̻�������ֱ��Ƕ���![]() ��
��
��2����ѧУÿ���踶���ӵ��̻�����Ϊ0.35��Ԫ���Ҷ�Ϊ0.25��Ԫ��Ҫʹ��ε��̻��ܷ��ò�����8��Ԫ������Ӧ���żӹ��������죿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����![]() ���߶�
���߶�![]() ���е㣬
���е㣬![]() ��
��![]() .
.
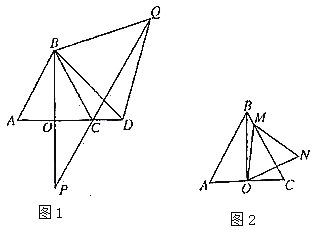
��1����ͼ1����![]() ����֤
����֤![]() �ǵȱ������Σ�
�ǵȱ������Σ�
��2����ͼ1���ڣ�1���������£�����![]() ������
������![]() �ϣ���
�ϣ���![]() �ڵ�
�ڵ�![]() �Ҳ࣬��
�Ҳ࣬��![]() �ǵȱ������Σ�
�ǵȱ������Σ�![]() ���ӳ��߽�ֱ��
���ӳ��߽�ֱ��![]() �ڵ�
�ڵ�![]() ����
����![]() �ij��ȣ�
�ij��ȣ�
��3����ͼ2���ڣ�1���������£�����![]() ���߶�
���߶�![]() �ϣ�
�ϣ�![]() �ǵȱ������Σ��ҵ�
�ǵȱ������Σ��ҵ�![]() �����߶�
�����߶�![]() �ӵ�
�ӵ�![]() �˶�����
�˶�����![]() ����
����![]() ��֮�˶������
��֮�˶������![]() ���˶�·���ij���.
���˶�·���ij���.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com