
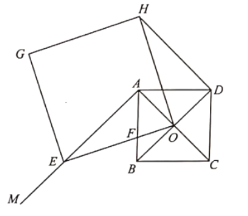
【题目】如图,已知正方形![]() 中,
中,![]() 相交于点
相交于点![]() ,过点
,过点![]() 作射线
作射线![]() ,点
,点![]() 是射线
是射线![]() 上一动点,连接
上一动点,连接![]() 交
交![]() 于点
于点![]() ,以
,以![]() 为一边,作正方形
为一边,作正方形![]() ,且点
,且点![]() 在正方形
在正方形![]() 的内部,连接
的内部,连接![]() .
.
(1)求证:![]() ;
;
(2)设![]() ,正方形
,正方形![]() 的边长为
的边长为![]() ,求
,求![]() 关于
关于![]() 的函数关系式,并写出定义域;
的函数关系式,并写出定义域;
(3)连接![]() ,当
,当![]() 是等腰三角形时,求
是等腰三角形时,求![]() 的长.
的长.
【答案】(1)详见解析;(2)![]() (
(![]() );(3)当
);(3)当![]() 是等腰三角形时,
是等腰三角形时,![]() 或
或![]()
【解析】
(1)根据正方形的性质得到∠AOD=90°,AO=OD,∠EOH=90°,OE=OH,由全等三角形的性质即可得到结论;
(2)如图1,过O作ON⊥AB于N,根据等腰直角三角形的性质得到![]() ,
,
根据勾股定理得到![]() ,根据平行线分线段成比例定理即可得到结论;
,根据平行线分线段成比例定理即可得到结论;
(3)①当AE=EG时,△AEG是等腰三角形,②当AE=AG时,△AEG是等腰三角形,如图2,过A作AP⊥EG于P③当GE=AG时,△AEG是等腰三角形,如图3,过G作GQ⊥AE于Q,根据相似三角形的性质或全等三角形的性质健即可得到结论.
(1)∵四边形![]() 是正方形,
是正方形,
![]() ,
,
![]() ,
,
∵四边形![]() 是正方形,
是正方形,
![]() ,
,
![]() ,
,
![]() ,
,
即![]() ,
,
![]() .
.
(2)如图1,过O作ON⊥AB于N,
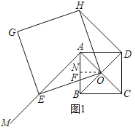
则![]() ,
,
∵BF=x,
∴AF=4-x,
∴FN=2-x,
∴![]() ,
,
∴![]() ,
,
∵AM⊥AC,
∴AE∥OB,
∴![]() ,
,
∴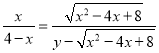 ,
,
∴![]() ;
;
(3)①当AE=EG时,△AEG是等腰三角形,则AE=OE,
∵∠EAO=90°,
∴这种情况不存在;
②当AE=AG时,△AEG是等腰三角形,
如图2,过A作AP⊥EG于P,则AP∥OE,
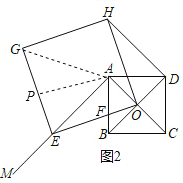
∴∠PAE=∠AEO,
∴△APE∽△EAO,
∴![]() ,
,
∵AE=AG,
∴![]() ,
,![]() ,
,
∴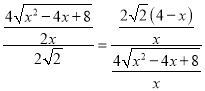 ,
,
解得:x=2,
②当GE=AG时,△AEG是等腰三角形,
如图3,过G作GQ⊥AE于Q,
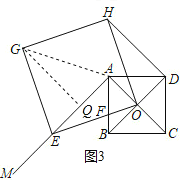
∴∠GQE=∠EAO=90°,
∴∠GEQ+∠EGQ=∠GEQ+∠AEO=90°,
∴∠EGQ=∠AEO,
∵GE=OE,
∴△EGQ≌△OEA(AAS),
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴BF=2或![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
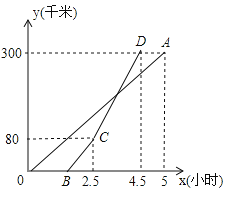
【题目】如图:甲、乙两地相距![]() ,一辆货车和一辆轿车先后从甲地出发驶向乙地,线段
,一辆货车和一辆轿车先后从甲地出发驶向乙地,线段![]() 和折线
和折线![]() 分别表示货车和轿车离甲地的距离
分别表示货车和轿车离甲地的距离![]()
![]() 与货车出发时间
与货车出发时间![]()
![]() 之间的函数关系,请根据图象解答下列问题:
之间的函数关系,请根据图象解答下列问题:
(1)货车的速度为___________![]() ,当轿车到达乙地后,货车距乙地的距离为____________千米;
,当轿车到达乙地后,货车距乙地的距离为____________千米;
(2)求轿车改变速度后![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)轿车到达乙地后,马上沿原路以![]() 段速度返回,求轿车从乙地出发后多长时间再次与货车相遇?
段速度返回,求轿车从乙地出发后多长时间再次与货车相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=∠ACB,以AC为直径的⊙O分别交AB、BC于点M、N,点P在AB的延长线上,且∠CAB=2∠BCP.
(1)求证:直线CP是⊙O的切线.
(2)若BC=2![]() ,sin∠BCP=
,sin∠BCP=![]() ,求点B到AC的距离.
,求点B到AC的距离.
(3)在第(2)的条件下,求△ACP的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.了解我区居民知晓“创建文明城区”的情况,适合全面调查;
B.甲乙两人跳高成绩的方差分别为![]() ,说明乙的距离成绩比甲稳定;
,说明乙的距离成绩比甲稳定;
C.一组数据2,2,3,4的众数是2,中位数是2.5;
D.可能性是1%的事件在一次试验中一定不会发生.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验,先在公路旁选一点C,再在笔直的车道a上确定点D,使CD⊥a,测得CD=42米,在a上点D的同侧取点A、B,使∠CAD=30 o,∠CBD=45o.
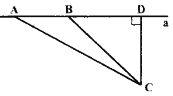
(1)求AB的长(结果保留根号);
(2)若本路段对汽车限速为60km/h,现测得某汽车从A到B用时2秒,这辆汽车是否超速?说明理由.(参考数据![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴,
轴,![]() 轴分别相交于
轴分别相交于![]() ,
,![]() 两点,与反比例函数
两点,与反比例函数![]() 的图象交于点
的图象交于点![]() ,点
,点![]() 的横坐标为4.
的横坐标为4.
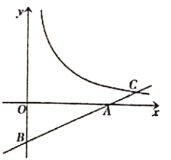
(1)求![]() 的值;
的值;
(2)过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,点
,点![]() 是该反比例函数
是该反比例函数![]() 的图象上一点,连接
的图象上一点,连接![]() ,
,![]() ,且
,且![]() .
.
①求点![]() 的坐标;
的坐标;
②求点![]() 到直线
到直线![]() 的距离
的距离![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某通信公司实行的部分套餐资费标准如下:
套餐类型 | 月费 (元/月) | 套餐内包含内容 | 套餐外资费 | ||
国内数据流量(MB) | 国内主叫(分钟) | 国内流量 | 国内主叫 | ||
套餐1 | 18 | 100 | 0 | 0.29元/MB | 0.19元/分钟 |
套餐2 | 28 | 100 | 50 | ||
套餐3 | 38 | 300 | 50 | ||
套餐4 | 48 | 500 | 50 | ||
小明每月大约使用国内数据流量200MB,国内主叫200分钟,若想使每月付费最少,则他应预定的套餐是( )
A.套餐1B.套餐2C.套餐3D.套餐4
查看答案和解析>>
科目:初中数学 来源: 题型:
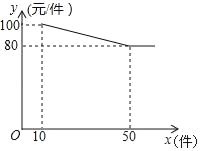
【题目】服装厂批发某种服装,每件成本为65元,规定不低于10件可以批发,其批发价y(元/件)与批发数量x(件)(x为正整数)之间所满足的函数关系如图所示.
(1)求y与x之间所满足的函数关系式,并写出x的取值范围;
(2)设服装厂所获利润为w(元),若10≤x≤50(x为正整数),求批发该种服装多少件时,服装厂获得利润最大?最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com