
分析 根据分子分母同乘以有理化因式进行分析整理,再列出不等式组进行解答即可.
解答 解:原式=$\frac{2-\sqrt{2}}{4-2}$+$\frac{3\sqrt{2}-2\sqrt{3}}{18-12}$+…+$\frac{(n+1)\sqrt{n}-n\sqrt{n+1}}{(n+1)^{2}n-{n}^{2}(n+1)}$,
=1-$\frac{\sqrt{2}}{2}$+$\frac{\sqrt{2}}{2}$-$\frac{\sqrt{3}}{3}$-$\frac{\sqrt{3}}{3}$-$\frac{\sqrt{4}}{4}$+…+$\frac{\sqrt{n}}{n}$-$\frac{\sqrt{n+1}}{n+1}$,
=1-$\frac{\sqrt{n+1}}{n+1}$,
∵它的值大于$\frac{19}{20}$,小于$\frac{20}{21}$,
∴可得1-$\frac{\sqrt{n+1}}{n+1}$>$\frac{19}{20}$①,
1-$\frac{\sqrt{n+1}}{n+1}$<$\frac{20}{21}$②,
由①②联立不等式组,解得:307≤n≤441
即正整数n的最大值是441,最小值是307.
∴441-307=134.
故答案是:134.
点评 此题考查分母有理化问题,注意分子分母同乘以有理化因式是解题关键.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:填空题
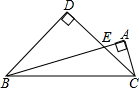 如图,△ABC是直角三角形,∠ABC=15°,∠BAC=90°,以BC为斜边作等腰直角△BDC,若BC=2$\sqrt{3}$,则△BEC的面积是3-$\sqrt{3}$.
如图,△ABC是直角三角形,∠ABC=15°,∠BAC=90°,以BC为斜边作等腰直角△BDC,若BC=2$\sqrt{3}$,则△BEC的面积是3-$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com