
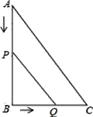
【题目】如图,在Rt△ABC中,∠B=90°,AC=10cm,BC=6cm,现有两点P、Q的分别从点A和点C同时出发,沿边AB,CB向终点B移动.已知点P,Q的速度分别为2cm/s,1cm/s,且当其中一点到达终点时,另一点也随之停止移动,设P,Q两点移动时间为xs.问是否存在这样的x,使得四边形APQC的面积等于16cm2?若存在,请求出此时x的值;若不存在,请说明理由.
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如果三角形的两个内角α与β满足2α+β=90°,那么我们称这样的三角形为“准互余三角形”.
(1)若△ABC是“准互余三角形”,∠C>90°,∠A=60°,则∠B= °;
(2)如图①,在Rt△ABC中,∠ACB=90°,AC=4,BC=5.若AD是∠BAC的平分线,不难证明△ABD是“准互余三角形”.试问在边BC上是否存在点E(异于点D),使得△ABE也是“准互余三角形”?若存在,请求出BE的长;若不存在,请说明理由.
(3)如图②,在四边形ABCD中,AB=7,CD=12,BD⊥CD,∠ABD=2∠BCD,且△ABC是“准互余三角形”,求对角线AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果抛物线C1的顶点在抛物线C2上,同时,抛物线C2的顶点在抛物线C1上,那么我们称抛物线C1与C2关联.
(1)已知抛物线C1:y=﹣2x2+4x+3与C2:y=2x2+4x﹣1,请判断抛物线C1与抛物线C2是否关联,并说明理由.
(2)抛物线C1:![]() ,动点P的坐标为(t,2),将抛物线绕点P旋转180°得到抛物线C2,若抛物线C1与C2关联,求抛物线C2的解析式.
,动点P的坐标为(t,2),将抛物线绕点P旋转180°得到抛物线C2,若抛物线C1与C2关联,求抛物线C2的解析式.
(3)点A为抛物线C1:![]() 的顶点,点B为抛物线C1关联的抛物线的顶点,是否存在以AB为斜边的等腰直角三角形ABC,使其直角顶点C在直线x=﹣10上?若存在,求出C点的坐标;若不存在,请说明理由.
的顶点,点B为抛物线C1关联的抛物线的顶点,是否存在以AB为斜边的等腰直角三角形ABC,使其直角顶点C在直线x=﹣10上?若存在,求出C点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年的9月3日是中国人民抗日战争胜利纪念日,某红色旅游景区为纪念抗日战争胜利73周年,今年9~10月份,对团体购买门票实行优惠,决定在原定票价基础上每张降价16元,这样按原定票价需花费2000元购买的门票张数,现在只花费了1200元.
(1)求每张门票的原定票价;
(2)根据实际情况,该景区决定对网上购票的个人也采取优惠,原定票价经过连续两次降价后票价为每张32.4元,求原定票价平均每次的下降率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图像与
的图像与![]() 轴交于
轴交于![]() 和
和![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,点
,点![]() 、
、![]() 是二次函数图像上的一对对称点,一次函数的图像经过
是二次函数图像上的一对对称点,一次函数的图像经过![]() 、
、![]() ;
;
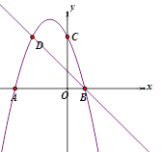
(1)请直接写出![]() 点的坐标;
点的坐标;
(2)求二次函数的解析式;
(3)根据图像直接写出使一次函数值大于二次函数值的![]() 的取值范围;
的取值范围;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某花圃用花盆培育某种花苗,经过实验发现每盆的盈利与每盆的株数构成一定的关系.每盆植入3株时,平均单株盈利3元;以同样的栽培条件,若每盆增加1株,平均单株盈利就减少0.5元.要使每盆的盈利达到10元,每盆应该植多少株?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,点C的坐标为(0,3),点A在x轴的负半轴上,点D、M分别在边AB、OA上,且AD=2DB,AM=2MO,一次函数y=kx+b的图象过点D和M,反比例函数y=![]() 的图象经过点D,与BC的交点为N.
的图象经过点D,与BC的交点为N.
(1)求反比例函数和一次函数的解析式;
(2)若点P在直线DM上,且使△OPM的面积与四边形OMNC的面积相等,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接与⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于AC点E,交PC于点F,连接AF.
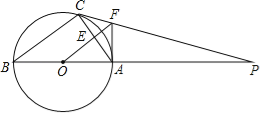
(1)判断AF与⊙O的位置关系并说明理由;
(2)若⊙O的半径为4,AF=3,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=2x2+bx+c经过(﹣3,0),(1,0)两点
(1)求抛物线的解析式,并求出其开口方向和对称轴
(2)用配方法求出该抛物线的顶点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com