
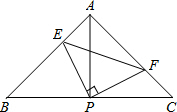
 如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,给出以下四个结论:①AE=CF; ②△EPF是等腰直角三角形; ③S四边形AEPF=
如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,给出以下四个结论:①AE=CF; ②△EPF是等腰直角三角形; ③S四边形AEPF=| 1 |
| 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
|
| 1 |
| 2 |


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
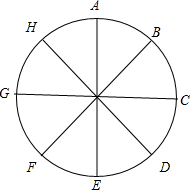 如图,A、B、C、D、E、F、G、H是圆形道路均分的8个点,甲、乙两人同时在道路的A点相背而行,已知甲的速度比乙快,经过5分钟后甲、乙两人在D点相遇,则又经过50分钟以后,两人应在哪里相遇?
如图,A、B、C、D、E、F、G、H是圆形道路均分的8个点,甲、乙两人同时在道路的A点相背而行,已知甲的速度比乙快,经过5分钟后甲、乙两人在D点相遇,则又经过50分钟以后,两人应在哪里相遇?查看答案和解析>>
科目:初中数学 来源: 题型:
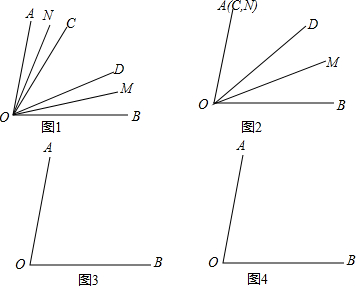 如图1,已知∠AOB=80°,∠COD=40°,OM平分∠BOD,ON平分∠AOC
如图1,已知∠AOB=80°,∠COD=40°,OM平分∠BOD,ON平分∠AOC查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com