
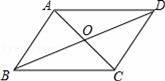
如图,在平行四边形ABCD中,连接对角线AC、BD,图中的全等三角形的对数( )


A.1对 B.2对 C.3对 D.4对
D【分析】平行四边形的性质是:对边相互平行且相等,对角线互相平分.这样不难得出:AD=BC,AB=CD,AO=CO,DO=BO,再利用“对顶角相等”就很容易找到全等的三角形:△ACD≌△CAB(SSS),△ABD≌△CDB(SSS),△AOD≌△COB(SAS),△AOB≌△COD(SAS).
【解答】解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC;OD=OB,OA=OC;
∵在△AOD和△COB中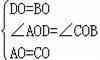

∴△AOD≌△COB(SAS);
同理可得出△AOB≌△COD(SAS);
∵在△ABD和△DCB中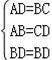
 ,
,
∴△ABD≌△CDB(SSS);
同理可得:△ACD≌△CAB(SSS).
共有4对全等三角形.
故选D.

【点评】考查了平行四边形的性质和全等三角形的判定,三角形全等的条件有时候是直接给的,有时候是根据已知条件推出的,还有时是由已知图形的性质得出的,做题时要全面考虑.


科目:初中数学 来源: 题型:
阳光通过窗口AB照射到室内,在地面上留下2.7米的亮区DE(如图所示),已知亮区到窗口下的墙角的距离EC=8.7米,窗口高AB=1.8米,则窗口底边离地面的高BC为( )
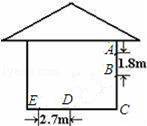

A.4米 B.3.8米 C.3.6米 D.3.4米
查看答案和解析>>
科目:初中数学 来源: 题型:
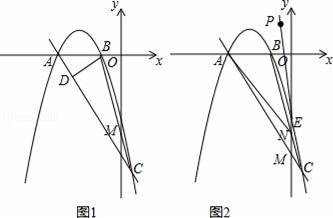
图1中,二次函数y=﹣ax2﹣4ax﹣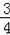
 的图象c交x轴于A,B两点(A在B的左侧),过A点的直线
的图象c交x轴于A,B两点(A在B的左侧),过A点的直线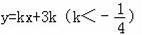
 交c于另一点C(x1,y1),交y轴于M.
交c于另一点C(x1,y1),交y轴于M.
(1)求点A的坐标,并求二次函数的解析式;
(2)过点B作BD⊥AC交AC于D,若M(0,﹣3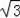
 )且Q点是直线AC上的一个动点.求出当△DBQ与△AOM相似时点Q的坐标;
)且Q点是直线AC上的一个动点.求出当△DBQ与△AOM相似时点Q的坐标;
(3)设P(﹣1,2),图2中连CP交二次函数的图象于另一点E(x2,y2),连AE交y轴于N.OM•ON是否是一个定值?如果是定值,求出该值;若不是,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com