
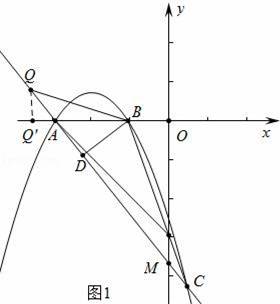
ͼ1�У����κ���y=��ax2��4ax��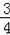
 ��ͼ��c��x����A��B���㣨A��B����ࣩ����A���ֱ��
��ͼ��c��x����A��B���㣨A��B����ࣩ����A���ֱ��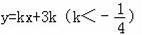
 ��c����һ��C��x1��y1������y����M��
��c����һ��C��x1��y1������y����M��
��1�����A�����꣬������κ����Ľ���ʽ��
��2������B��BD��AC��AC��D����M��0����3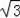
 ����Q����ֱ��AC�ϵ�һ�����㣮�������DBQ���AOM����ʱ��Q�����ꣻ
����Q����ֱ��AC�ϵ�һ�����㣮�������DBQ���AOM����ʱ��Q�����ꣻ
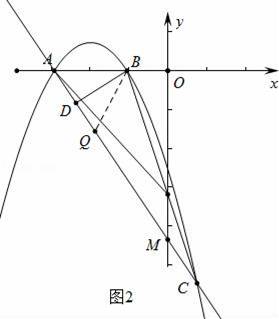
��3����P����1��2����ͼ2����CP�����κ�����ͼ������һ��E��x2��y2������AE��y����N��OM•ON�Ƿ���һ����ֵ������Ƕ�ֵ�������ֵ�������ǣ���˵�����ɣ�
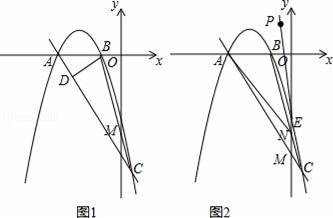

�����㡿���κ����ۺ��⣮
����������1����ֱ��y=kx+3k�����A���꣬���������߽���ʽ���ɽ�����⣮
��2���������������ۢ���ͼ1�У���Q��DA���ӳ�����ʱ����BQD=30�㣬��BQD����AOM���ڵ�Q���A�غ�ʱ����BQD=60���DQB����OAM������ͼ2�У���Q���߶�DC��ʱ����BQD=60�㣬��DQB����OAM������ͼ3�У�����BQD=30��ʱ����DQB����OMA�ֱ��ֱ�������μ��ɣ�
��3�����ֱ��PC�Ľ���ʽ������������ɷ����������E���꣬�����ֱ��AE�������N���꣬��k��ʾOM��ON���ɽ�����⣮
����𡿣�1���⣺y=0��kx+3k=0��֮��x=��3������A����3��0����
��ΪA����3��0����y=��ax2��4ax��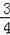
 ������0=��9a+12a��
������0=��9a+12a��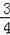
 ��
��
��֮�ɵ�a=
 ��
��
���Ըö��κ����ı���ʽy=��
 x2��x��
x2��x��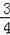
 ��
��
��2����Rt��AOM��OA=3��OM=3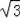
 tan��OAM=
tan��OAM=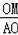
 =
=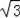
 �����ԡ�OAM=60�㣬
�����ԡ�OAM=60�㣬
����ͼ1�У���Q��DA���ӳ�����ʱ����BQD=30�㣬��BQD�ס�AOM��
��Rt��ABD��BD=BA��sin60��=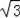
 ��
��
��Rt��BQD��BD=OQ��sin30��=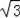
 �����BQ=2
�����BQ=2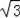
 ��
��
��Q����QQ���x�ᴹ��ΪQ�䣬
�ߡ�BAD=60��=��BQA+��QBA����BQD=30�㣬
���QBQ��=30�㣬
��RT��BQQ���У��ߡ�QBQ��=30�㣬BQ=2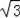
 ��
��
QQ��=
 ��BQ��=3��
��BQ��=3��
����Q����4��
 ����
����
�ڵ�Q���A�غ�ʱ����BQD=60���DQB�ס�OAM���˵�Q����3��0����
����ͼ2�У���Q���߶�DC��ʱ����BQD=60�㣬��DQB�ס�OAM��
�ڡ�AQB�У���BAQ=��AQB=60�㣬
��BQ=AB=2��
����Q����2����
 ����
����
����ͼ3�У�����BQD=30��ʱ����DQB�ס�OMA����ʱBQ��OM
��Q����1��y����ֱ��y=��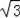
 x��3
x��3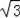
 ���ϣ����y=��2
���ϣ����y=��2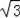
 ��
��
�Ӷ�Q����1����2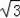
 ����
����
����������Q����4��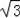
 ����Q����3��0����Q����2����
����Q����3��0����Q����2����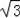
 ����Q����1����2
����Q����1����2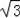
 ����
����
��3����ͼ4�У�ֱ��y=kx+3k����κ���y=��
 x2��x��
x2��x��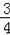
 ͼ��Ľ�����A��C���㣬
ͼ��Ľ�����A��C���㣬
����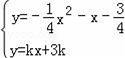
 �������ɵ�
�������ɵ�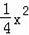
 +��k+1��x+��
+��k+1��x+��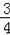
 +3k��=0��
+3k��=0��
����ΪA����3��0����C��x1��y1����
����x1=��4k��1��y1=��4k2+2k��
����P����1��2�����C��ֱ�ߣ�Y=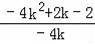
 x+
x+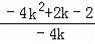
 +2��
+2��
ֱ��PC�������ߵĽ��㣬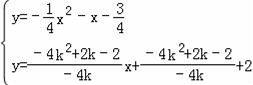
 ����ȥy�����õ���
����ȥy�����õ���

 x2+��1+
x2+��1+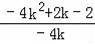
 ��x+
��x+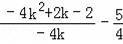
 =0��
=0��
��x2+x1=x2+����4k��1��=��
 ��
��
��x2=��1��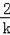
 ��y2=
��y2=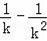
 ��
��
��ֱ��AEΪy=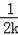
 x+
x+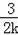
 ��
��
��OM=��3k��ON=��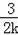
 ��
��
��OM•ON=����3k������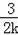
 ��=
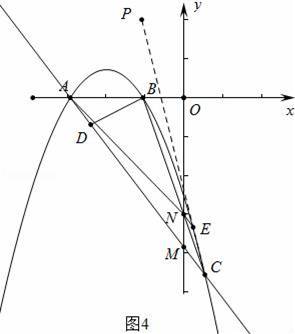
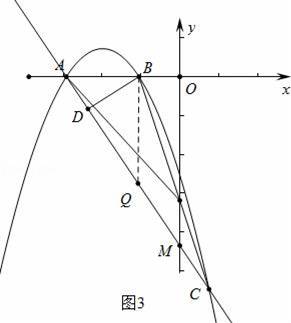
��=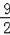
 ��
��
��OM•ON�Ƕ�ֵ�������ֵ��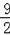
 ��
��




�����������⿼����κ������й�֪ʶ�����������ε��ж������ʡ�ֱ��������30�Ƚǵ����ʵ�֪ʶ��ѧ�����ϵ����ȷ����������ʽ�ǽ���Ĺؼ���ѧ���ò�����ʾֱ�߽���ʽ��������꣬���շ������۵�˼�룬�����п�ѹ���⣮
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
��֪����x��һԪ���η���x2+mx+n=0������ʵ�����ֱ�Ϊx1=a��x2=b��a��b��������κ���y=x2+mx+n�У���y��0ʱ��x��ȡֵ��Χ�ǣ�������
A��x��a B��x��b C��a��x��b D��x��a��x��b
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
���м��㣺��1��an•an=2an����2��a6+a6=a12����3��c•c5=c5����4��26+26=27����5����3xy3��3=9x3y9�У���ȷ�ĸ���Ϊ��������
A��0�� B��1�� C��2�� D��3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ�Ƕ��κ���y=ax2+bx+c�IJ���ͼ����ͼ���֪����ʽax2+bx+c��0�Ľ⼯�ǣ�������
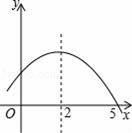

A����1��x��5 B��x��5 C��x����1��x��5 D��x����1��x��5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ����ƽ���ı���ABCD�У����ӶԽ���AC��BD��ͼ�е�ȫ�������εĶ�����������


A��1�� B��2�� C��3�� D��4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
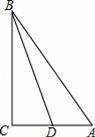
��Rt��ACB�У���C=90�㣬��D��AC���е㣬cos��CBD=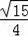
 ����sin��ABD=��������������
����sin��ABD=��������������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
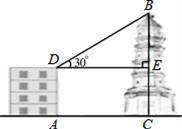
����ͼ����¥AD����BC����ֱ�ڵ���AC����¥AD��50�ף��ʹ�¥AD���90��C����һ��BC��ij����¥��D���������B�����ǡ�BDE=30�㣬�ҡ�BED=90�㣬������BC������������������ο����ݣ�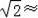
 1.41��
1.41��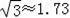
 ��
��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
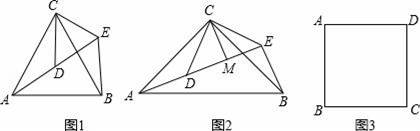
��1�����ⷢ��
��ͼ1����ACB�͡�DCE��Ϊ�ȱ������Σ���A��D��E��ͬһֱ���ϣ�����BE��
��գ�
�١�AEB�Ķ���Ϊ��������������
���߶�AD��BE֮���������ϵΪ��������������
��2����չ̽��
��ͼ2����ACB�͡�DCE��Ϊ����ֱ�������Σ���ACB=��DCE=90�㣬��A��D��E��ͬһֱ���ϣ�CMΪ��DCE��DE���ϵĸߣ�����BE�����жϡ�AEB�Ķ������߶�CM��AE��BE֮���������ϵ����˵�����ɣ�
��3���������
��ͼ3����������ABCD�У�CD=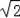
 ������P����PD=1���ҡ�BPD=90�㣬��ֱ��д����A��BP�ľ��룮
������P����PD=1���ҡ�BPD=90�㣬��ֱ��д����A��BP�ľ��룮

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com