练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

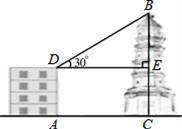
    ．如图，大楼AD和塔BC都垂直于地面AC，大楼AD高50米，和大楼AD相距90米的C处有一塔BC，某人在楼顶D处测得塔顶B的仰角∠BDE=30°，且∠BED=90°，求塔高BC．（结果保留整数，参考数据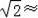： 1.41，）


    【考点】解直角三角形的应用-仰角俯角问题．

    【分析】在直角△BDE中利用三角函数求得BE的长，然后加上EC即可求得．

    【解答】解：∵在Rt△BDE中，tan∠BDE=，DE=90，

    ∴BE=DE×tan30°=30（米），

    又∵BC=BE+CE=50+30≈1.73

    ∴BC≈50+51.9≈102（米）．

    答：塔BC高度约为102米．

    【点评】本题考查仰角的定义，要求学生能借助仰角构造直角三角形并解直角三角形．

    　


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

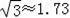
    科目：初中数学 来源： 题型：


    先阅读再解题．

    题目：如果（x﹣1）5=a1x5+a2x4+a3x3+a4x2+a5x+a6，求a6的值．

    解这类题目时，可根据等式的性质，取x的特殊值，如x=0，1，﹣1…代入等式两边即可求得有关代数式的值．如：当x=0时，（0﹣1）5=a6，即a6=1．

    请你求出下列代数式的值．

    （1）a1+a2+a3+a4+a5

    （2）a1﹣a2+a3﹣a4+a5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在矩形AOBC中，点A的坐标是（﹣2，1），点C的纵坐标是4，则B、C两点的坐标分别是　　　　　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


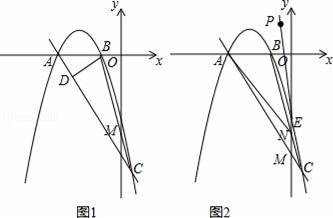
    图1中，二次函数y=﹣ax2﹣4ax﹣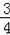的图象c交x轴于A，B两点（A在B的左侧），过A点的直线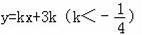交c于另一点C（x1，y1），交y轴于M．

    （1）求点A的坐标，并求二次函数的解析式；

    （2）过点B作BD⊥AC交AC于D，若M（0，﹣3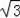）且Q点是直线AC上的一个动点．求出当△DBQ与△AOM相似时点Q的坐标；

    （3）设P（﹣1，2），图2中连CP交二次函数的图象于另一点E（x2，y2），连AE交y轴于N．OM•ON是否是一个定值？如果是定值，求出该值；若不是，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知x1，x2是方程x2﹣=0的两根，若实数a满足a+x1+x2﹣x1•x2=2018，则a=　　　　　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    分解因式．a+2ab+ab2=　　　　　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    函数y=中，自变量x的取值范围是（　　）

    A．x＞﹣1     B．x＜﹣1     C．x≠﹣1      D．x≠0

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    PM2.5是指大气中直径小于或等于0.0000025m的颗粒物，将0.0000025用科学记数法表示为　　　　　　．

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，将三角尺的直角顶点放在直尺的一边上，∠1=30°，∠2=125°，则∠3等于(      )

    A．15°　　　       B．25° 　　   　   C．35°    　　   D．45°    

     


    查看答案和解析>>

    同步练习册答案