
(1)问题发现
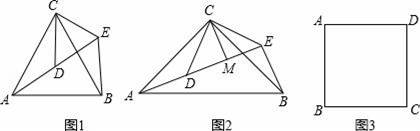
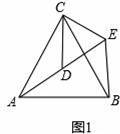
如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.
填空:
①∠AEB的度数为 ;
②线段AD,BE之间的数量关系为 .
(2)拓展探究
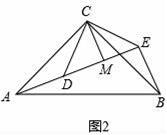
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.
(3)解决问题
如图3,在正方形ABCD中,CD=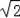
 ,若点P满足PD=1,且∠BPD=90°,请直接写出点A到BP的距离.
,若点P满足PD=1,且∠BPD=90°,请直接写出点A到BP的距离.

【考点】圆的综合题;全等三角形的判定与性质;等腰三角形的性质;等边三角形的性质;直角三角形斜边上的中线;正方形的性质;圆周角定理.
【专题】综合题;压轴题;探究型.
【分析】(1)由条件易证△ACD≌△BCE,从而得到:AD=BE,∠ADC=∠BEC.由点A,D,E在同一直线上可求出∠ADC,从而可以求出∠AEB的度数.
(2)仿照(1)中的解法可求出∠AEB的度数,证出AD=BE;由△DCE为等腰直角三角形及CM为△DCE中DE边上的高可得CM=DM=ME,从而证到AE=2CH+BE.
(3)由PD=1可得:点P在以点D为圆心,1为半径的圆上;由∠BPD=90°可得:点P在以BD为直径的圆上.显然,点P是这两个圆的交点,由于两圆有两个交点,接下来需对两个位置分别进行讨论.然后,添加适当的辅助线,借助于(2)中的结论即可解决问题.
【解答】解:(1)①如图1,
∵△ACB和△DCE均为等边三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=60°.
∴∠ACD=∠BCE.
在△ACD和△BCE中,
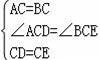

∴△ACD≌△BCE(SAS).
∴∠ADC=∠BEC.
∵△DCE为等边三角形,
∴∠CDE=∠CED=60°.
∵点A,D,E在同一直线上,
∴∠ADC=120°.
∴∠BEC=120°.
∴∠AEB=∠BEC﹣∠CED=60°.
故答案为:60°.
②∵△ACD≌△BCE,
∴AD=BE.
故答案为:AD=BE.
(2)∠AEB=90°,AE=BE+2CM.
理由:如图2,
∵△ACB和△DCE均为等腰直角三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=90°.
∴∠ACD=∠BCE.
在△ACD和△BCE中,
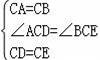

∴△ACD≌△BCE(SAS).
∴AD=BE,∠ADC=∠BEC.
∵△DCE为等腰直角三角形,
∴∠CDE=∠CED=45°.
∵点A,D,E在同一直线上,
∴∠ADC=135°.
∴∠BEC=135°.
∴∠AEB=∠BEC﹣∠CED=90°.
∵CD=CE,CM⊥DE,
∴DM=ME.
∵∠DCE=90°,
∴DM=ME=CM.
∴AE=AD+DE=BE+2CM.
(3)点A到BP的距离为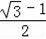
 或
或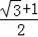
 .
.
理由如下:
∵PD=1,
∴点P在以点D为圆心,1为半径的圆上.
∵∠BPD=90°,
∴点P在以BD为直径的圆上.
∴点P是这两圆的交点.
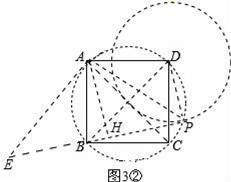
①当点P在如图3①所示位置时,
连接PD、PB、PA,作AH⊥BP,垂足为H,
过点A作AE⊥AP,交BP于点E,如图3①.
∵四边形ABCD是正方形,
∴∠ADB=45°.AB=AD=DC=BC=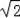
 ,∠BAD=90°.
,∠BAD=90°.
∴BD=2.
∵DP=1,
∴BP=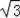
 .
.
∵∠BPD=∠BAD=90°,
∴A、P、D、B在以BD为直径的圆上,
∴∠APB=∠ADB=45°.
∴△PAE是等腰直角三角形.
又∵△BAD是等腰直角三角形,点B、E、P共线,AH⊥BP,
∴由(2)中的结论可得:BP=2AH+PD.
∴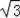
 =2AH+1.
=2AH+1.
∴AH=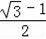
 .
.
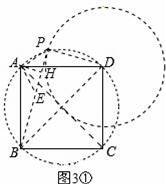
②当点P在如图3②所示位置时,
连接PD、PB、PA,作AH⊥BP,垂足为H,
过点A作AE⊥AP,交PB的延长线于点E,如图3②.
同理可得:BP=2AH﹣PD.
∴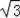
 =2AH﹣1.
=2AH﹣1.
∴AH=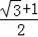
 .
.
综上所述:点A到BP的距离为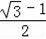
 或
或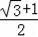
 .
.




【点评】本题考查了等边三角形的性质、正方形的性质、等腰三角形的性质、直角三角形斜边上的中线等于斜边的一半、圆周角定理、三角形全等的判定与性质等知识,考查了运用已有的知识和经验解决问题的能力,是体现新课程理念的一道好题.而通过添加适当的辅助线从而能用(2)中的结论解决问题是解决第(3)的关键.


 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源: 题型:
图1中,二次函数y=﹣ax2﹣4ax﹣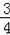
 的图象c交x轴于A,B两点(A在B的左侧),过A点的直线
的图象c交x轴于A,B两点(A在B的左侧),过A点的直线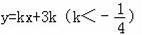
 交c于另一点C(x1,y1),交y轴于M.
交c于另一点C(x1,y1),交y轴于M.
(1)求点A的坐标,并求二次函数的解析式;
(2)过点B作BD⊥AC交AC于D,若M(0,﹣3
 )且Q点是直线AC上的一个动点.求出当△DBQ与△AOM相似时点Q的坐标;
)且Q点是直线AC上的一个动点.求出当△DBQ与△AOM相似时点Q的坐标;
(3)设P(﹣1,2),图2中连CP交二次函数的图象于另一点E(x2,y2),连AE交y轴于N.OM•ON是否是一个定值?如果是定值,求出该值;若不是,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
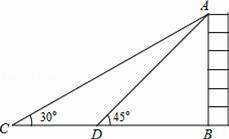
如图,某校数学兴趣小组为测得大厦AB的高度,在大厦前的平地上选择一点C,测得大厦顶端A的仰角为30°,再向大厦方向前进80米,到达点D处(C、D、B三点在同一直线上),又测得大厦顶端A的仰角为45°,请你计算该大厦的高度.(精确到0.1米,参考数据: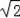
 ≈1.414,
≈1.414,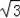
 ≈1.732)
≈1.732)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com