
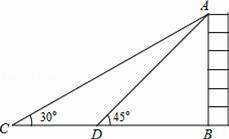
如图,某校数学兴趣小组为测得大厦AB的高度,在大厦前的平地上选择一点C,测得大厦顶端A的仰角为30°,再向大厦方向前进80米,到达点D处(C、D、B三点在同一直线上),又测得大厦顶端A的仰角为45°,请你计算该大厦的高度.(精确到0.1米,参考数据: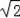
 ≈1.414,
≈1.414,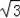
 ≈1.732)
≈1.732)

【考点】解直角三角形的应用-仰角俯角问题.
【分析】先设AB=x;根据题意分析图形:本题涉及到两个直角三角形Rt△ACB和Rt△ADB,应利用其公共边BA构造等量关系,解三角形可求得DB、CB的数值,再根据CD=BC﹣BD=80,进而可求出答案.
【解答】解:设AB=x,
在Rt△ACB和Rt△ADB中,
∵∠C=30°,∠ADB=45°,CD=80
∴DB=x,AC=2x,BC=
 =
=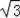
 x,
x,
∵CD=BC﹣BD=80,
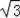
 x﹣x=80,
x﹣x=80,
∴x=40(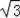
 +1)≈109.3米.
+1)≈109.3米.
答:该大厦的高度是109.3米.
【点评】本题考查俯角、仰角的定义,要求学生能借助俯角、仰角构造直角三角形并结合图形利用三角函数解直角三角形.


科目:初中数学 来源: 题型:
(1)问题发现
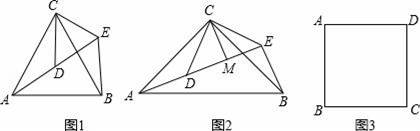
如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.
填空:
①∠AEB的度数为 ;
②线段AD,BE之间的数量关系为 .
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.
(3)解决问题
如图3,在正方形ABCD中,CD=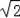
 ,若点P满足PD=1,且∠BPD=90°,请直接写出点A到BP的距离.
,若点P满足PD=1,且∠BPD=90°,请直接写出点A到BP的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,若锐角△ABC内接于⊙O,点D在⊙O外(与点C在AB同侧),则下列三个结论:①sin∠C>sin∠D;②cos∠C>cos∠D;③tan∠C>tan∠D中,正确的结论为( )
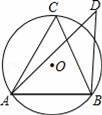

A.①② B.②③ C.①②③ D.①③
查看答案和解析>>
科目:初中数学 来源: 题型:
某校动漫社团有20名学生代表学校参加市级“动漫设计”比赛,他们的得分情况如表:
| 人数 | 4 | 6 | 8 | 2 |
| 分数 | 80 | 85 | 90 | 95 |
那么这20名学生所得分数的众数和中位数分别是( )
A.95和85 B.90和85 C.90和87.5 D.85和87.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com