
如图,若锐角△ABC内接于⊙O,点D在⊙O外(与点C在AB同侧),则下列三个结论:①sin∠C>sin∠D;②cos∠C>cos∠D;③tan∠C>tan∠D中,正确的结论为( )
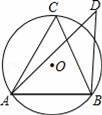

A.①② B.②③ C.①②③ D.①③
科目:初中数学 来源: 题型:
.数学活动课上,老师提出这样一个问题:如果AB=BC,∠ABC=60°,∠APC=30°,连接PB,那么PA、PB、PC之间会有怎样的等量关系呢?经过思考后,部分同学进行了如下的交流:
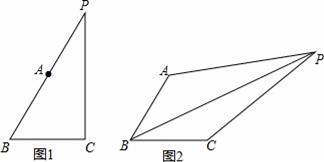
小蕾:我将图形进行了特殊化,让点P在BA延长线上(如图1),得到了一个猜想:PA2+PC2=PB2.
小东:我假设点P在∠ABC的内部,根据题目条件,这个图形具有“共端点等线段”的特点,可以利用旋转解决问题,旋转△PAB后得到△P′CB,并且可推出△PBP′,△PCP′分别是等边三角形、直角三角形,就能得到猜想和证明方法.
这时老师对同学们说,请大家完成以下问题:
(1)如图2,点P在∠ABC的内部,
①PA=4,PC=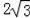
 ,PB= .
,PB= .
②用等式表示PA、PB、PC之间的数量关系,并证明.
(2)对于点P的其他位置,是否始终具有②中的结论?若是,请证明;若不是,请举例说明.

查看答案和解析>>
科目:初中数学 来源: 题型:
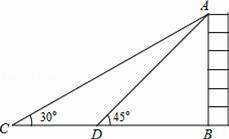
如图,某校数学兴趣小组为测得大厦AB的高度,在大厦前的平地上选择一点C,测得大厦顶端A的仰角为30°,再向大厦方向前进80米,到达点D处(C、D、B三点在同一直线上),又测得大厦顶端A的仰角为45°,请你计算该大厦的高度.(精确到0.1米,参考数据: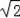
 ≈1.414,
≈1.414,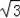
 ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣5,1),B(﹣2,2),C(﹣1,4),请按下列要求画图:
(1)将△ABC先向右平移4个单位长度、再向下平移1个单位长度,得到△A1B1C1,画出△A1B1C1;
(2)△A2B2C2与△ABC关于原点O成中心对称,画出△A2B2C2.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com