
已知关于x的一元二次方程x2+mx+n=0的两个实数根分别为x1=a,x2=b(a<b),则二次函数y=x2+mx+n中,当y<0时,x的取值范围是( )
A.x<a B.x>b C.a<x<b D.x<a或x>b
科目:初中数学 来源: 题型:
下列说法正确的个数是( )
①无理数都是无限小数;
②4的平方根是2;
③
 =a;
=a;
④等腰三角形底边上的中线、高线、角平分线互相重合;
⑤坐标平面内的点与有序实数对一一对应.
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,过点A与x轴平行的直线交抛物线y=
 于点B、C,线段BC的长度为6,抛物线y=﹣2x2+b与y轴交于点A,则b=( )
于点B、C,线段BC的长度为6,抛物线y=﹣2x2+b与y轴交于点A,则b=( )


A.1 B.4.5 C.3 D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
为提高运输效率、保障高峰时段人们的顺利出行,地铁公司在保证安全运行的前提下,缩短了发车间隔,从而提高了运送乘客的数量.缩短发车间隔后比缩短发车间隔前平均每分钟多运送乘客50人,使得缩短发车间隔后运送14400人的时间与缩短发车间隔前运送12800人的时间相同,那么缩短发车间隔前平均每分钟运送乘客多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
先阅读再解题.
题目:如果(x﹣1)5=a1x5+a2x4+a3x3+a4x2+a5x+a6,求a6的值.
解这类题目时,可根据等式的性质,取x的特殊值,如x=0,1,﹣1…代入等式两边即可求得有关代数式的值.如:当x=0时,(0﹣1)5=a6,即a6=1.
请你求出下列代数式的值.
(1)a1+a2+a3+a4+a5
(2)a1﹣a2+a3﹣a4+a5.
查看答案和解析>>
科目:初中数学 来源: 题型:
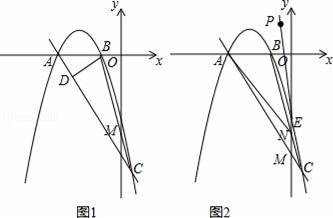
图1中,二次函数y=﹣ax2﹣4ax﹣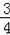
 的图象c交x轴于A,B两点(A在B的左侧),过A点的直线
的图象c交x轴于A,B两点(A在B的左侧),过A点的直线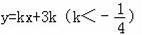
 交c于另一点C(x1,y1),交y轴于M.
交c于另一点C(x1,y1),交y轴于M.
(1)求点A的坐标,并求二次函数的解析式;
(2)过点B作BD⊥AC交AC于D,若M(0,﹣3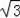
 )且Q点是直线AC上的一个动点.求出当△DBQ与△AOM相似时点Q的坐标;
)且Q点是直线AC上的一个动点.求出当△DBQ与△AOM相似时点Q的坐标;
(3)设P(﹣1,2),图2中连CP交二次函数的图象于另一点E(x2,y2),连AE交y轴于N.OM•ON是否是一个定值?如果是定值,求出该值;若不是,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com