为提高运输效率、保障高峰时段人们的顺利出行，地铁公司在保证安全运行的前提下，缩短了发车间隔，从而提高了运送乘客的数量．缩短发车间隔后比缩短发车间隔前平均每分钟多运送乘客50人，使得缩短发车间隔后运送14400人的时间与缩短发车间隔前运送12800人的时间相同，那么缩短发车间隔前平均每分钟运送乘客多少人？
【考点】分式方程的应用．
【分析】首先设缩短发车间隔前平均每分钟运送乘客x人，则缩短发车间隔后平均每分钟运送乘客（x+50）人，根据关键语句“缩短发车间隔后运送14400人的时间与缩短发车间隔前运送12800人的时间相同，”可得方程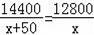
，再解分式方程即可，注意不要忘记检验．
【解答】解：设缩短发车间隔前平均每分钟运送乘客x人．…
根据题意，得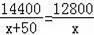
，…
解得x=400．…
经检验，x=400是原方程的解．…
答：缩短发车间隔前平均每分钟运送乘客400人．
【点评】此题主要考查了分式方程的应用，关键是弄清题意，设出未知数，找准题目中的等量关系，列出分式方程．列分式方程解应用题的一般步骤：设、列、解、验、答，必须严格按照这5步进行做题，规范解题步骤，另外还要注意完整性：如设和答叙述要完整，要写出单位等．
举一反三同步巧讲精练系列答案
口算与应用题卡系列答案
名师点睛字词句段篇系列答案科目：初中数学 来源： 题型：
【探究】：某商场秋季计划购进一批进价为每条40元的围巾进行销售根据销售经验，应季销售时，若每条围巾的售价为60元，则可售出400条；若每条围巾的售价每提高1元，销售量相应减少10条．
（1）假设每条围巾的售价提高x元，那么销售每条围巾所获得的利润是 元，销售量是 条（用含x的代数式表示）．
（2）设应季销售利润为y元，请写y与x的函数关系式；并求出应季销售利润为8000元时每条围巾的售价．
【拓展】：根据销售经验，过季处理时，若每条围巾的售价定为30元亏本销售，可售出50条；若每条围巾的售价每降低1元，销售量相应增加5条，
（1）若剩余100条围巾需要处理，经过降价处理后还是无法销售的只能积压在仓库，损失本金；若使亏损金额最小，每条围巾的售价应是 元．
（2）若过季需要处理的围巾共m条，且100≤m≤300，过季亏损金额最小是 元；（用含m的代数式表示）
【延伸】：若商场共购进了500条围巾且销售情况满足上述条件，如果应季销售利润在不低于8000元的条件下：
（1）没有售出的围巾共m条，则m的取值范围是： ；
（2）要使最后的总利润（销售利润=应季销售利润﹣过季亏损金额）最大，则应季销售的售价是 元．
参考公式：抛物线y=ax2+bx+c（a≠0）的顶点坐标是
．
查看答案和解析>>
科目：初中数学 来源： 题型：
已知关于x的一元二次方程x2+mx+n=0的两个实数根分别为x1=a，x2=b（a＜b），则二次函数y=x2+mx+n中，当y＜0时，x的取值范围是（ ）
A．x＜a B．x＞b C．a＜x＜b D．x＜a或x＞b
查看答案和解析>>
科目：初中数学 来源： 题型：
如图是二次函数y=ax2+bx+c的部分图象，由图象可知不等式ax2+bx+c＜0的解集是（ ）
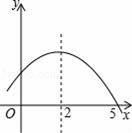
A．﹣1＜x＜5 B．x＞5 C．x＜﹣1且x＞5 D．x＜﹣1或x＞5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
|+|
﹣2|+
．
B．
C．
D．
