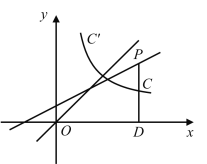
【题目】如图，过直线
上一点
作
轴于点
，线段
交函数
的图像于点
，点为线段的中点，点关于直线
的对称点
的坐标为
．
（1）求
、
的值；
（2）求直线与函数图像的交点坐标；
（3）直接写出不等式
的解集．
【答案】（1）3，
；（2）（2，
）；（3）0＜x＜
【解析】
（1）根据点C′在反比例函数图像上求出m值，利用对称性求出点C的坐标，从而得出点P坐标，代入一次函数表达式求出k值；
（2）将两个函数表达式联立，得到一元二次方程，求解即可；
（3）根据（2）中交点坐标，结合图像得出结果.
解：（1）∵C′的坐标为(1，3)，
代入
中，
得：m=1×3=3，
∵C和C′关于直线y=x对称，
∴点C的坐标为（3，1），
∵点C为PD中点，
∴点P（3，2），
将点P代入
，
∴解得：k=；
∴k和m的值分别为：3，；
（2）联立：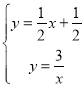
，得：
，
解得：
，
（舍），
∴直线与函数图像的交点坐标为（2，）；
（3）∵两个函数的交点为：（2，），
由图像可知：当0＜x＜时，反比例函数图像在一次函数图像上面，
∴不等式
的解集为：0＜x＜.
科目：初中数学 来源： 题型：
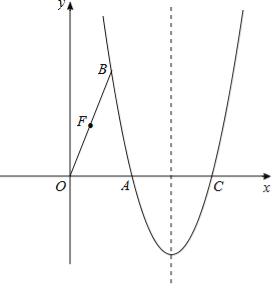
【题目】如图，在平面直角坐标系中，抛物线
经过点A（
，0）和点B（1，
），与x轴的另一个交点为C．
（1）求抛物线的函数表达式；
（2）点D在对称轴的右侧，x轴上方的抛物线上，且∠BDA=∠DAC，求点D的坐标；
（3）在（2）的条件下，连接BD，交抛物线对称轴于点E，连接AE．
①判断四边形OAEB的形状，并说明理由；
②点F是OB的中点，点M是直线BD的一个动点，且点M与点B不重合，当∠BMF=
∠MFO时，请直接写出线段BM的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
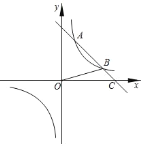
【题目】如图，在平面直角坐标系xOy中，一次函数y＝﹣x+4的图象与反比例函数y＝
（k＞0）的图象相交于A，B两点，与x轴相交于点C，连接OB，且
BOC的面积为2．则k=______．
查看答案和解析>>
科目：初中数学 来源： 题型：
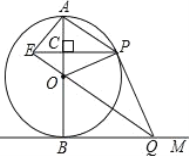
【题目】如图，AB是⊙O的直径，BM切⊙O于点B，点P是⊙O上的一个动点（点P不与A，B两点重合），连接AP，过点O作OQ∥AP交BM于点Q，过点P作PE⊥AB于点C，交QO的延长线于点E，连接PQ，OP，AE．
（1）判断直线PQ与⊙O的关系；
（2）若直径AB的长为4．当四边形AEOP为菱形时，求PE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，菱形
中，
，动点
以每秒
个单位的速度自点
出发沿线段
运动到点
，同时动点
以每秒
个单位的速度自点出发沿折线
运动到点
．图2是点、运动时，
的面积
随时间
变化关系图象，则
的值是（ ）
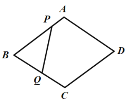
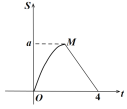
图1 图2
A.B.
C.
D.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在图1，2，3中，已知
，
，点
为线段
上的动点，连接
，以为边向上作菱形
，且
．
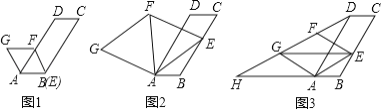
（1）如图1，当点与点
重合时，
________°；
（2）如图2，连接
．
①填空：
_________
（填“>”，“<”，“=”）；
②求证：点
在
的平分线上；
（3）如图3，连接
，
，并延长交
的延长线于点
，当四边形
是平行四边形时，求
的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
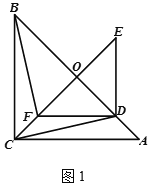
【题目】阅读材料：如图
，
与
都是等腰直角三角形
，且点
在
边上，，
的中点均为
，连接
，
，
，显然，点
，
，在同一条直线上，可以证明
，所以
解决问题：
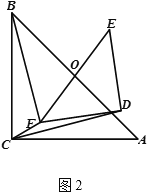
（1） 将图中的
绕点旋转到图
的位置， 猜想此时线段与的数量关系，并证明你的结论．
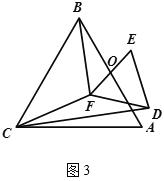
（2） 如图
，若与都是等边三角形，，的中点均为，上述
中结论仍然成立吗？如果成立，请说明理由；如果不成立，请求出与之间的数量关系．
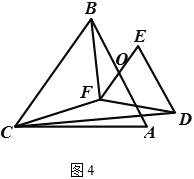
（3） 如图
， 若与都是等腰三角形，，的中点均为，且顶角
，与之间的数量关系如何（用含
的式子表示出来）？请直接写出结果．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
