
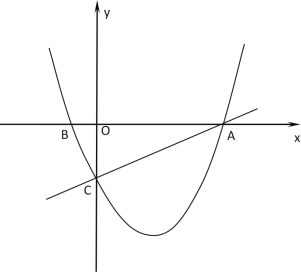
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��![]() ��x�ύ�ڵ�A����y�ύ�ڵ�C��������
��x�ύ�ڵ�A����y�ύ�ڵ�C��������![]() ����A��C���㣬��x�����һ����Ϊ��B��
����A��C���㣬��x�����һ����Ϊ��B��
(1)�������ߵĺ�������ʽ��
(2)��DΪֱ��AC�·���������һ���㣻
������CD���Ƿ���ڵ�D��ʹ��ACƽ�֡�OCD�������ڣ����D�ĺ����ꣻ�������ڣ���˵�����ɣ�
���ڢٵ������£���PΪ��������λ��AC�·���һ�����㣬��P��C��A��DΪ������ı����������S����Sȡ��ֵ����ʲô��Χʱ����Ӧ�ĵ�P����ֻ��2����
���𰸡�(1)![]() ��(2)�ٴ��ڣ���
��(2)�ٴ��ڣ���![]() �ĺ�����Ϊ
�ĺ�����Ϊ![]() ����
����![]()
��������
��1���������A��C���꣬�ٸ��ݴ���ϵ������⼴�ɣ�
��2���������ڵ�D��ʹ��ACƽ�֡�OCD�����OCA=��DCA������D��DE��x���ڵ�E����ֱ��AC�ڵ�F����ͼ1����DE��y�ᣬ��DC=DF����D��m��![]() ��������ú�m�Ĵ���ʽ��ʾ��DF��Ȼ�����DC=DF���ɵó�����m�ķ��̣��ⷽ�̼��ý����
��������ú�m�Ĵ���ʽ��ʾ��DF��Ȼ�����DC=DF���ɵó�����m�ķ��̣��ⷽ�̼��ý����
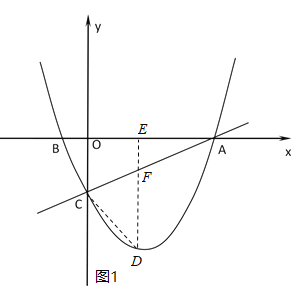
���������Ľ��������D���������ACD�������Ȼ��ֵ�P��ֱ��CD�·�ʱ����PG��x���ڵ�G����ֱ��CD�ڵ�Q����ͼ2�����ö��κ��������������PCD������������һ�����������������Pʱ��S��ֵ����P��ֱ��AD�·�ʱ��������������ͼ3���������PAD�������������������ֻ��һ����Pʱ��S��ֵ�����ǿɵý����
�⣺��1����![]() ����y=0ʱ��x=4�����A��4��0����
����y=0ʱ��x=4�����A��4��0����
��x=0ʱ��y=��2�����C��0����2����
��A��C�������������![]() �ã�
�ã�
![]() ����ã�
����ã�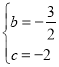 ��
��
�������ߵĽ���ʽ��![]() ��
��
��2���������ڵ�D��ʹ��ACƽ�֡�OCD�����OCA=��DCA��
����D��DE��x���ڵ�E����ֱ��AC�ڵ�F����ͼ1����DE��y�ᣬ
���OCA=��DFC�����DCF=��DFC����DC=DF��
��D��m��![]() ������F��m��
������F��m��![]() ����
����
��![]() ��
��
��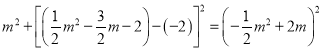 ��
��
��ã�![]() ����ȥ����
����ȥ����![]() ��
��
����ڵ�D��ʹ��ACƽ�֡�OCD���ҵ�D�ĺ�������![]() ��
��
��3����![]() ����x=
����x=![]() ʱ��
ʱ��![]() �����D�������ǣ�
�����D�������ǣ�![]() ��
��![]() ����
����
��ʱDF=![]() ����ACD�����=
����ACD�����=![]() ��
��
����P��ֱ��CD�·�ʱ����PG��x���ڵ�G����ֱ��CD�ڵ�Q����ͼ2��
�ߵ�C��0����2����D��![]() ��
��![]() ����
����
��ֱ��CD�Ľ���ʽΪ![]() ��
��
���P�������ǣ�n��![]() ������Q��n��
������Q��n��![]() ����
����
��![]() ��
��
���PCD��������=![]() ��
��
��ʱ�ı���CPDA�����=![]() ��
��
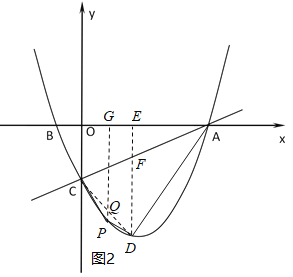
����P��ֱ��AD�·�ʱ����PG��x���ڵ�G����ֱ��CD�ڵ�Q����ͼ3��
�ߵ�A��4��0����D��![]() ��
��![]() ����
����
��ֱ��AD�Ľ���ʽΪ![]() ��
��
���P�������ǣ�n��![]() ������Q��n��
������Q��n��![]() ����
����
��![]() ��
��
���PAD��������=![]() ��
��
��ʱ�ı���CDPA�����=![]() ��
��
���ϣ���S��ȡֵ��ΧΪ![]() ����Ӧ�ĵ�P����ֻ��2����
����Ӧ�ĵ�P����ֻ��2����




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����12�֣�ʵʩ�¿γ̸ĸ��ѧ��������ѧϰ���������������кܴ���ߣ�����ʦΪ���˽����̰༶ѧ������ѧϰ�����������ľ���������Ա��ಿ��ѧ��������Ϊ�������µĸ��ٵ��飬�����������ֳ����࣬A���ر�ã�B���ã�C��һ�㣻D���ϲ�������������Ƴ�����������������ͳ��ͼ���������ͳ��ͼ����������⣺

��1�����ε����У�����ʦһ�������� ��ͬѧ������C��Ů���� ����D�������� ����
��2�������������ͳ��ͼ����������
��3��Ϊ�˹�ͬ����������ʦ��ӱ������A���D��ѧ���зֱ�ѡȡһλͬѧ���С�һ��һ������ѧϰ�������б���������ͼ�ķ��������ѡ��λͬѧǡ����һλ��ͬѧ��һλŮͬѧ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijũ��Ʒ��˾��![]() Ԫ�ijɱ��չ���ij��ũ��Ʒ
Ԫ�ijɱ��չ���ij��ũ��Ʒ![]() �֣�Ŀǰ������
�֣�Ŀǰ������![]() Ԫ/�ֵļ۸�ֱ���۳�.���ù�˾������ũ��Ʒ���������ִ�����ʽ�ɹ�ѡ��
Ԫ/�ֵļ۸�ֱ���۳�.���ù�˾������ũ��Ʒ���������ִ�����ʽ�ɹ�ѡ��
��ʽһ����˾�ɽ�����ũ��Ʒֱ����![]() Ԫ/�ֵļ۸��۳���ʣ�µ�ȫ���ӹ��ɰ��Ʒ���ۣ��ӹ��ɱ����Բ��ƣ���ÿ�ָ�ũ��Ʒ���Լӹ��õ�
Ԫ/�ֵļ۸��۳���ʣ�µ�ȫ���ӹ��ɰ��Ʒ���ۣ��ӹ��ɱ����Բ��ƣ���ÿ�ָ�ũ��Ʒ���Լӹ��õ�![]() �ֵİ��Ʒ��ÿ�ְ��Ʒ���ۼ�Ϊ
�ֵİ��Ʒ��ÿ�ְ��Ʒ���ۼ�Ϊ![]() Ԫ.
Ԫ.
��ʽ������˾������ũ��Ʒȫ����������������ÿ���ڻ���ʧ![]() �֣���ÿ������֧�����ַ���
�֣���ÿ������֧�����ַ���![]() Ԫ����ͬʱÿ����ÿ�ֵļ۸�����
Ԫ����ͬʱÿ����ÿ�ֵļ۸�����![]() Ԫ.
Ԫ.
��1�����ù�˾ѡȡ��ʽһ��������ũ��Ʒ�����ջ����![]() �������ʣ���ù�˾ֱ�������˶��ٶ�ũ��Ʒ��
�������ʣ���ù�˾ֱ�������˶��ٶ�ũ��Ʒ��
��2�����ù�˾ѡȡ��ʽ����������ũ��Ʒ�����ջ���1![]() Ԫ�������ũ��Ʒ�����˶��ٸ����ڲų��ۣ�
Ԫ�������ũ��Ʒ�����˶��ٸ����ڲų��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() Ϊ���κ���
Ϊ���κ���![]() ͼ��Ķ��㣬ֱ��
ͼ��Ķ��㣬ֱ��![]() �ֱ�
�ֱ�![]() ��ĸ������
��ĸ������![]() ���ڵ�
���ڵ�![]() ����
����![]() ��
��
(1)�����κ���ͼ����![]() ������κ����Ľ���ʽ��
������κ����Ľ���ʽ��
(2)��ͼ������![]() ����Ϊ
����Ϊ![]() ���ҵ�
���ҵ�![]() ��
��![]() �ڲ�(�������߽�)��
�ڲ�(�������߽�)��
����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
������![]() ��
��![]() ���ڶ��κ���ͼ���ϣ��ԱȽ�
���ڶ��κ���ͼ���ϣ��ԱȽ�![]() ��
��![]() �Ĵ�С
�Ĵ�С

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ŀǰ���ҹ��Ŀ��������õ��˴���ȵ���ߣ������������ij����1���µĿ�������������������Ľ�����Ƴ����µ�������������ͳ��ͼ��
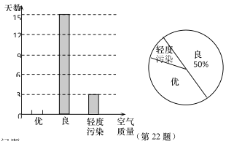
�����ͼ���ṩ����Ϣ�������������⣺
��1�����ε����У�һ�����������Ϊ_______�죻����ͼ�У���ʾ�������Ⱦ�������ε�Բ�Ľ�Ϊ______�ȣ�
��2��������ͼ����������
��3�����Ƹó���һ�꣨��365����㣩�У���������δ�ﵽ�ŵ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���Ծ���ABCD�ı�CDΪֱ������O����E��AB ���е㣬����CE����O�ڵ�F������AF���ӳ���BC�ڵ�H��
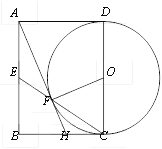
��1��������AO�����ж��ı���AECO����״����˵�����ɣ�
��2����֤��AH�ǡ�O�����ߣ�
��3����AB��6��CH��2����AH�ij�Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƶ����С��Թ�ũ���о���ƶ��������ũ��һ���л���̬ˮ���ؿ����г�����ȥ����ȣ���������ˮ���IJ���������1000ǧ�ˣ�ÿǧ�˵�ƽ�������۱�ȥ�꽵����1Ԫ�����������ܶ��ȥ��������![]() ��
��
��1����֪ȥ������ˮ�����������ܶ�Ϊ10��Ԫ��������ˮ������ÿǧ�˵�ƽ���������Ƕ���Ԫ��
��2��ijˮ����ӹ�ũ��ֱ��������רӪ����ˮ�������鷢�֣���ÿǧ�˵�ƽ�����ۼ�Ϊ41Ԫ����ÿ����۳�300ǧ�ˣ���ÿǧ�˵�ƽ�����ۼ�ÿ����3Ԫ��ÿ��ɶ�����180ǧ�ˣ���ˮ����һ�������Ϊ![]() Ԫ����ÿǧ�˵�ƽ�����ۼ�Ϊ����Ԫʱ����ˮ����һ������������������Ƕ��٣����������ʱ���������ú��Բ��ƣ���
Ԫ����ÿǧ�˵�ƽ�����ۼ�Ϊ����Ԫʱ����ˮ����һ������������������Ƕ��٣����������ʱ���������ú��Բ��ƣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
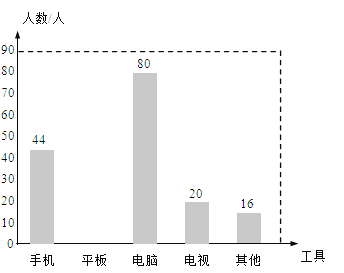
����Ŀ���ڡ�ͣ�β�ͣѧ���ڼ䣬ijУ��ѧ��ȤС��Ա�Уͬѧ�ۿ���ѧ��Ƶ��ʹ�õĹ��߽����˵��飬�����������ȡ�������ݽ��з�����������������Ƴ���������������ͳ�Ʊ���ͳ��ͼ��
���� | ���� | Ƶ�� |
�ֻ� | 44 | a |
ƽ�� | b | 0.2 |
���� | 80 | c |
���� | 20 | d |
��ȷ�� | 16 | 0.08 |
�����������Ϣ�ش��������⣺
��1������ȡ������ͬѧ���� ���ˣ�����a���� ����b���� ����
��2���벹ȫ����ͳ��ͼ��
��3������У�ۿ���ѧ��Ƶ��ѧ��������Ϊ2500�ˣ���ʹ�õ��Ե�ѧ������Լ�� ���ˣ�![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���O��ԭ�㣬����OABC�Ķ���A��x����������ϣ�����C��y���������ϣ���B�������ǣ�5��3����������![]() ����A��C���㣬��x�����һ�������ǵ�D������BD��
����A��C���㣬��x�����һ�������ǵ�D������BD��
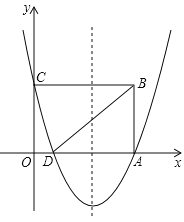
��1���������ߵĽ���ʽ��
��2����M�������߶Գ����ϵ�һ�㣬��M��B��DΪ����������ε������6�����M�����ꣻ
��3����P�ӵ�D��������ÿ��1����λ���ȵ��ٶ���D��B�����˶���ͬʱ��Q�ӵ�B��������ÿ��1����λ���ȵ��ٶ���B��A��D�����˶�������P�����Bʱ��P��Qͬʱֹͣ�˶������˶���ʱ��Ϊt�룬��tΪ��ֵʱ����D��P��QΪ������������ǵ��������Σ���ֱ��д�����з���������ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com