
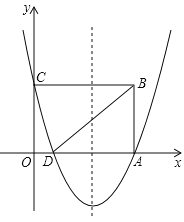
【题目】如图,在平面直角坐标系中,点O是原点,矩形OABC的顶点A在x轴的正半轴上,顶点C在y的正半轴上,点B的坐标是(5,3),抛物线![]() 经过A、C两点,与x轴的另一个交点是点D,连接BD.
经过A、C两点,与x轴的另一个交点是点D,连接BD.
(1)求抛物线的解析式;
(2)点M是抛物线对称轴上的一点,以M、B、D为顶点的三角形的面积是6,求点M的坐标;
(3)点P从点D出发,以每秒1个单位长度的速度沿D→B匀速运动,同时点Q从点B出发,以每秒1个单位长度的速度沿B→A→D匀速运动,当点P到达点B时,P、Q同时停止运动,设运动的时间为t秒,当t为何值时,以D、P、Q为顶点的三角形是等腰三角形?请直接写出所有符合条件的值.
【答案】(1) ![]()
(2) M (3,![]() )或(3,
)或(3,![]() )
)
(3)当t=![]() 或t=
或t=![]() 或t=
或t=![]() 时,以D、P、Q为顶点的三角形是等腰三角形.
时,以D、P、Q为顶点的三角形是等腰三角形.
【解析】
(1)求出点A、C的坐标,利用待定系数法求出抛物线的解析式.
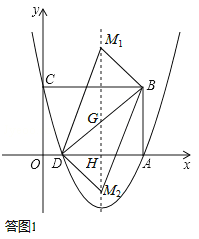
(2)如答图1所示,关键是求出MG的长度,利用面积公式解决;注意,符合条件的点M有2个,不要漏解.
(3)△DPQ为等腰三角形,可能有三种情形,需要分类讨论:
①若PD=PQ,如答图2所示;②若PD=DQ,如答图3所示;③若PQ=DQ,如答图4所示.
解:(1)∵矩形ABCD,B(5,3),∴A(5,0),C(0,3).
∵点A(5,0),C(0,3)在抛物线![]() 上,
上,
∴ ,
,
解得: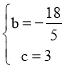 .
.
∴抛物线的解析式为:![]() .
.
(2)∵![]() ,
,
∴抛物线的对称轴为直线x=3.
如答图1所示,设对称轴与BD交于点G,与x轴交于点H,则H(3,0).
令y=0,即![]() ,
,
解得x=1或x=5.
∴D(1,0).
∴DH=2,AH=2,AD=4.
∵![]() ,
,
∴GH=DHtan∠ADB=2×![]() =
=![]() .
.
∴G(3,![]() ).
).
∵S△MBD=6,即S△MDG+S△MBG=6,
∴![]() MGDH+
MGDH+![]() MGAH=6,
MGAH=6,
即:![]() MG×2+
MG×2+![]() MG×2=6.
MG×2=6.
解得:MG=3.
∴点M的坐标为(3,![]() )或(3,
)或(3,![]() ).
).
(3)在Rt△ABD中,AB=3,AD=4,则BD=5,
∴sinB=![]() ,cosB=
,cosB=![]() .
.
以D、P、Q为顶点的三角形是等腰三角形,则:
①若PD=PQ,如答图2所示,

此时有PD=PQ=BQ=t,过点Q作QE⊥BD于点E,
则BE=PE,BE=BQcosB=![]() t,QE=BQsinB=
t,QE=BQsinB=![]() t,
t,
∴DE=t+![]() t=
t=![]() t.
t.
由勾股定理得:DQ2=DE2+QE2=AD2+AQ2,
即(![]() t)2+(
t)2+(![]() t)2=42+(3﹣t)2,整理得:11t2+6t﹣25=0,
t)2=42+(3﹣t)2,整理得:11t2+6t﹣25=0,
解得:t=![]() 或t=﹣5(舍去).
或t=﹣5(舍去).
∴t=![]() .
.
②若PD=DQ,如答图3所示,

此时PD=t,DQ=AB+AD﹣t=7﹣t,
∴t=7﹣t.
∴t=![]() .
.
③若PQ=DQ,如答图4所示,
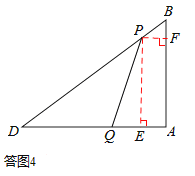
∵PD=t,
∴BP=5﹣t.
∵DQ=7﹣t,
∴PQ=7﹣t,AQ=4﹣(7﹣t)=t﹣3.
过点P作PF⊥AB于点F,
则PF=PBsinB=(5﹣t)×![]() =4﹣
=4﹣![]() t,BF=PBcosB=(5﹣t)×
t,BF=PBcosB=(5﹣t)×![]() =3﹣
=3﹣![]() t.
t.
∴AF=AB﹣BF=3﹣(3﹣![]() t)=
t)=![]() t.
t.
过点P作PE⊥AD于点E,则PEAF为矩形,
∴PE=AF=![]() t,AE=PF=4﹣
t,AE=PF=4﹣![]() t.
t.
∴EQ=AQ﹣AE=(t﹣3)﹣(4﹣![]() t)=
t)=![]() t﹣7.
t﹣7.
在Rt△PQE中,由勾股定理得:EQ2+PE2=PQ2,即:(![]() t﹣7)2+(
t﹣7)2+(![]() t)2=(7﹣t)2,
t)2=(7﹣t)2,
整理得:13t2﹣56t=0,解得:t=0(舍去)或t=![]() .
.
∴t=![]() .
.
综上所述,当t=![]() 或t=
或t=![]() 或t=
或t=![]() 时,以D、P、Q为顶点的三角形是等腰三角形.
时,以D、P、Q为顶点的三角形是等腰三角形.


科目:初中数学 来源: 题型:
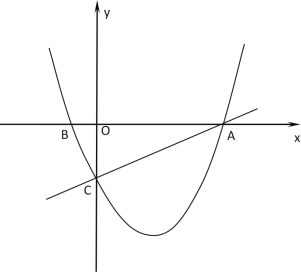
【题目】如图,在平面直角坐标系中,直线![]() 与x轴交于点A,与y轴交于点C,抛物线
与x轴交于点A,与y轴交于点C,抛物线![]() 经过A、C两点,与x轴的另一交点为点B.
经过A、C两点,与x轴的另一交点为点B.
(1)求抛物线的函数表达式;
(2)点D为直线AC下方抛物线上一动点;
①连接CD,是否存在点D,使得AC平分∠OCD?若存在,求点D的横坐标;若不存在,请说明理由.
②在①的条件下,若P为抛物线上位于AC下方的一个动点,以P、C、A、D为顶点的四边形面积记作S,则S取何值或在什么范围时,相应的点P有且只有2个?
查看答案和解析>>
科目:初中数学 来源: 题型:
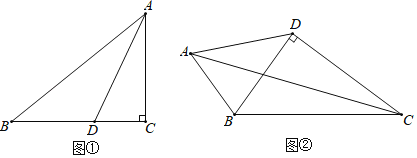
【题目】如果三角形的两个内角α与β满足2α+β=90°,那么我们称这样的三角形为“准互余三角形”.
(1)若△ABC是“准互余三角形”,∠C>90°,∠A=60°,则∠B= °;
(2)如图①,在Rt△ABC中,∠ACB=90°,AC=4,BC=5.若AD是∠BAC的平分线,不难证明△ABD是“准互余三角形”.试问在边BC上是否存在点E(异于点D),使得△ABE也是“准互余三角形”?若存在,请求出BE的长;若不存在,请说明理由.
(3)如图②,在四边形ABCD中,AB=7,CD=12,BD⊥CD,∠ABD=2∠BCD,且△ABC是“准互余三角形”,求对角线AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋中,有四个完全相同的小球,把它们分别标号为1,﹣2,3,4,随机摸取一个小球记下标号后放回,再随机摸取一个小球记下标号,则两次摸取的小球的标号之积为负数的概率为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=![]() +bx+c经过△ABC的三个顶点,其中点A(0,﹣1),点B(9,﹣10),AC∥x轴,点P是直线AC上方抛物线上的动点.
+bx+c经过△ABC的三个顶点,其中点A(0,﹣1),点B(9,﹣10),AC∥x轴,点P是直线AC上方抛物线上的动点.
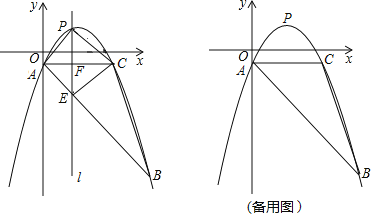
(1)求抛物线的解析式;
(2)过点P且与y轴平行的直线l与直线AB,AC分别交于点E,F,当四边形AECP的面积最大时,求点P的坐标;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C,P,Q为顶点的三角形与△ABC相似?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于点A(﹣3,m+8),B(n,﹣6)两点.
的图象交于点A(﹣3,m+8),B(n,﹣6)两点.
(1)求一次函数与反比例函数的解析式;
(2)求△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“只要人人都献出一点爱,世界将变成美好的人间”,在新型肺炎疫情期间,全国人民万众一心,众志成城,共克时艰.某社区积极发起“援鄂捐款”活动倡议,有2500名居民踊跃参与献爱心.社区管理员随机抽查了部分居民捐款情况,统计图如图:

(1)计算本次共抽查居民人数,并将条形图补充完整;
(2)根据统计情况,请估计该社区捐款20元以上(含20元)的居民有多少人?
(3)该社区有1名男管理员和3名女管理员,现要从中随机挑选2名管理员参与“社区防控”宣讲活动,请用列表法或树状图法求出恰好选到“1男1女”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
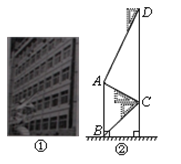
【题目】腾飞中学在教学楼前新建了一座“腾飞”雕塑(如图11①).为了测量雕塑的高度,小明在二楼找到一点C,利用三角板测得雕塑顶端A点的仰角为30°,底部B点的俯角为45°,小华在五楼找到一点D,利用三角板测得A点的俯角为60°(如图10②).若已知CD为10米,请求出雕塑AB的高度.(结果精确到0.1米,参考数据![]() =1.73)
=1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里,装有四个分别标有数字1,2,3,4的小球,它们的形状、大小、质地等完全相同.小米先从盒子中随机取出一个小球,记下数字为x,且不放回盒子,再由小华随机取出一个小球,记下数字为y.
(1)用列表法或画树状图表示出(x,y)的所有可能出现的结果;
(2)求小米、小华各取一次小球所确定的点(x,y)落在反比例函数y=![]() 的图象上的概率.
的图象上的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com