
【题目】某校为了了解全校400名学生参加课外锻炼的情况,随机对40名学生一周内平均每天参加课外锻炼的时间进行了调查,结果如下:(单位:分)
40 21 35 24 40 38 23 52 35 62
36 15 51 45 40 42 40 32 43 36
34 53 38 40 39 32 45 40 50 45
40 40 26 45 40 45 35 40 42 45
(1)补全频率分布表和频率分布直方图.
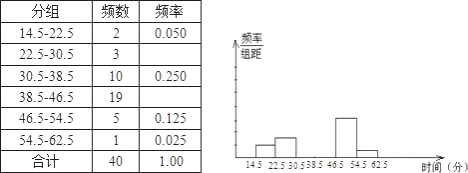
(2)填空:在这个问题中,总体是_____,样本是_____.由统计结果分析的,这组数据的平均数是38.35(分),众数是_____,中位数是______.
(3)如果描述该校400名学生一周内平均每天参加课外锻炼时间的总体情况,你认为用平均数、众数、中位数中的哪一个量比较合适?
【答案】(1)补全频率分布表和频率分布直方图,见解析;(2)总体是全校400名学生参加课外锻炼的时间,样本是40名学生一周内平均每天参加课外锻炼的时间;众数是40,中位数是40;(3)用平均数、中位数、或众数描述该校400名学生参加课外锻炼时间的总体情况都比较合适.
【解析】
(1)根据调查表,可补全频率分布表和频率分布直方图;
(2)根据总体、样本、众数、中位数的概念,可得答案;
(3)因为在这一问题中,这三个量非常接近;所以用平均数、众数和中位数描述该校400名学生参加课外锻炼时间的总体情况都比较合适.
解:(1)补全频率分布表和频率分布直方图,
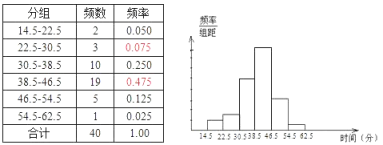
(2)总体是全校400名学生参加课外锻炼的时间,样本是40名学生一周内平均每天参加课外锻炼的时间;众数是40,中位数是40;
(3)在这一问题中,这三个量非常接近,所以用平均数、中位数、或众数描述该校400名学生参加课外锻时间的总体情况都比较合适.
故答案为:(1)补全频率分布表和频率分布直方图,见解析;(2)总体是全校400名学生参加课外锻炼的时间,样本是40名学生一周内平均每天参加课外锻炼的时间;众数是40,中位数是40;(3)用平均数、中位数、或众数描述该校400名学生参加课外锻炼时间的总体情况都比较合适.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形ABCD的顶点A的坐标为(﹣1,1),点B在x轴正半轴上,点D在第三象限的双曲线y=![]() 上,过点C作CE∥x轴交双曲线于点E,连接BE,则△BCE的面积为( )
上,过点C作CE∥x轴交双曲线于点E,连接BE,则△BCE的面积为( )
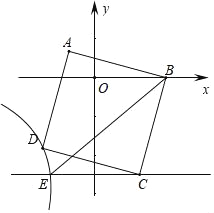
A. 5B. 6C. 7D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
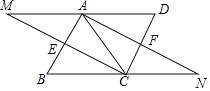
【题目】已知:如图,在平行四边形ABCD中,BC=AC,E,F分别是AB,CD的中点,连接CE并延长交DA的延长线于M,连接AF并延长交BC的延长线于N.
(1)求证:△ABN≌△CDM;
(2)当平行四边形ABCD的边或角满足什么关系时,四边形AECF是正方形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲进行了5次射击训练,平均成绩为9环,且前4次的成绩(单位:环)依次为:8,10,9,10.
(1)求甲第5次的射击成绩与这5次射击成绩的方差;
(2)乙在相同情况下也进行了5次射击训练,平均成绩为9环,方差为0.9环,请问甲和乙哪个的射击成绩更稳定?
查看答案和解析>>
科目:初中数学 来源: 题型:
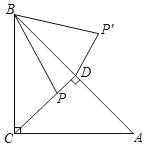
【题目】如图,在△ABC中,∠ACB=90°,AC=BC=4,P是△ABC的高CD上一个动点,以B点为旋转中心把线段BP逆时针旋转45°得到BP′,连接DP′,则DP′的最小值是( )
A.2![]() -2B.4﹣2
-2B.4﹣2![]() C.2﹣
C.2﹣![]() D.
D.![]() -1
-1
查看答案和解析>>
科目:初中数学 来源: 题型:
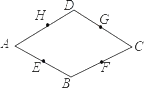
【题目】已知四边形ABCD为菱形,点E、F、G、H分别为各边中点,判断E、F、G、H四点是否在同一个圆上,如果在同一圆上,找到圆心,并证明四点共圆;如果不在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有三个质地、大小都相同的小球分别标上数字2,-2,3后放入一个不透明的口袋搅匀,任意摸出一个小球,记下数字a后,放回口袋中搅匀,再任意摸出一个小球,又记下数字b.这样就得到一个点的坐标(a,b).
(1)求这个点(a,b)恰好在函数y=-x的图像上的概率.(请用“画树状图”或“列表”等方法给出分析过程,并求出结果)
(2)如果再往口袋中增加n(n≥1)个标上数字2的小球,按照同样的操作过程,所得到的点(a,b)恰好在函数y=-x的图像上的概率是 (请用含n的代数式直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
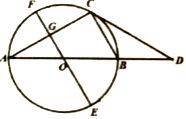
【题目】如图,⊙O是△ABC的外接圆,AB为⊙O的直径,过点C作∠BCD=∠CAB交AB的延长线于点D,过点O作直径EF∥BC,交AC于点G.
(1)求证:CD是⊙O的切线.
(2)若⊙O的半径为2,∠BCD=30°.
①连接AE、DE,求证:四边形ACDE是菱形.
②当点P是线段AD上的一动点时,求PF+PG的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com