练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，把一块长为40cm，宽为30cm的矩形硬纸板的四角剪去四个相同小正方形，然后把纸板的四边沿虚线折起，并用胶带粘好，即可做成一个无盖纸盒．若该无盖纸盒的底面积为600cm2，设剪去小正方形的边长为xcm，则可列方程为（　　）

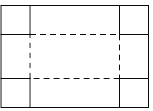
    A.（30﹣2x）（40﹣x）＝600B.（30﹣x）（40﹣x）＝600

    C.（30﹣x）（40﹣2x）＝600D.（30﹣2x）（40﹣2x）＝600

    【答案】D

    【解析】

    设剪去小正方形的边长是xcm，则纸盒底面的长为（40﹣2x）cm，宽为（30﹣2x）cm，根据长方形的面积公式结合纸盒的底面积是600cm2，即可得出关于x的一元二次方程，此题得解．

    解：设剪去小正方形的边长是xcm，则纸盒底面的长为（40﹣2x）cm，宽为（30﹣2x）cm，

    根据题意得：（40﹣2x）（30﹣2x）＝600．

    故选：D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】小王计划批发“山东大樱桃”和“泰国榴莲”两个品种的水果共120斤，樱桃和榴莲的批发价分别为32元/斤和40元/斤.设购买了樱桃x斤.

    （1）若小王批发这两种水果正好花费了4400元，那么小王分别购买了多少斤樱桃和榴莲？填写下表，并列方程求解；

    品种

    批发价（元）

    购买斤数

    小王应付的钱数（元）

    樱桃

    32

    x

    榴莲

    40

    （2）设小王购买两种水果的总花费为y元，试写出y与x之间的函数表达式.

    （3）若要求所批发的榴莲的斤数不少于樱桃斤数的2倍，那么购买樱桃的数量为多少时，可使小王的总花费最少？这个最少花费是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，甲楼AB高20米，乙楼CD高10米，两栋楼之间的水平距离BD＝30m，为了测量某电视塔EF的高度，小明在甲楼楼顶A处观测电视塔塔顶E，测得仰角为37°，小明在乙楼楼顶C处观测电视塔塔顶E，测得仰角为45°，求该电视塔的高度EF．

    （参考数据：sin37°≈0.6，cos37°≈0.8，tan37°≈0.75，）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在四边形ABCD中，∠A＝∠C＝90°，DE，BF分别平分∠ADC，∠ABC，并交线段AB，CD于点E，F（点E，B不重合）．在线段BF上取点M，N（点M在BN之间），使BM＝2FN．当点P从点D匀速运动到点E时，点Q恰好从点M匀速运动到点N．记QN＝x，PD＝y，已知，当Q为BF中点时，．

    （1）判断DE与BF的位置关系，并说明理由；

    （2）求DE，BF的长；

    （3）若AD＝6．①当DP＝DF时，通过计算比较BE与BQ的大小关系；②连结PQ，当PQ所在直线经过四边形ABCD的一个顶点时，求所有满足条件的x的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小寇随机调查了若干租用共享单车市民的骑车时间t（单位：分），将获得的据分成四组（A：0＜t≤10，B：10＜t≤20，C：20＜t≤30， D：t＞30），绘制了如下统计图，根据图中信息，解答下列问题：

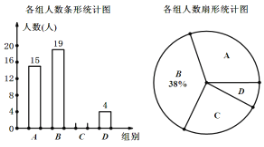
    （1）小寇调查的总人数是 人；

    （2）表示C组的扇形统计图的圆心角的度数是 °；

    （3）如果小寇想从D组的甲、乙、丙、丁四人中随机选择两人进一步了解平时租用共享单车情况，请用列表或画树状图的方法求出丁被选中的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，⊙O是△ABC的外接圆，∠BAC＝45°，AD⊥BC于点D，延长AD交⊙O于点E，若BD＝4，CD＝1，则DE的长是_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，已知函数y1＝x2+ax+1，y2＝x2+bx+2，y3＝x2+cx+4，其中a，b，c是正实数，且满足b2＝ac．设函数y1，y2，y3的图象与x轴的交点个数分别为M1，M2，M3，（　　）

    A.若M1＝2，M2＝2，则M3＝0B.若M1＝1，M2＝0，则M3＝0

    C.若M1＝0，M2＝2，则M3＝0D.若M1＝0，M2＝0，则M3＝0

    查看答案和解析>>

    科目：初中数学 来源： 题型：

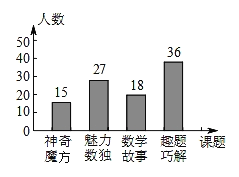
    【题目】为了培养学生数学学习兴趣，某校七年级准备开设“神奇魔方”、“魅力数独”、“数学故事”、“趣题巧解”四门选修课（每位学生必须且只选其中一门）．学校对七年级部分学生进行选课调查，得到如图所示的统计图．

    （1）根据统计图，本次选课共调查了　 　名学生；

    （2）若该校七年级有960名学生，请计算出选“神奇魔方”的人数；

    （3）学校将选“神奇魔方”的学生分成人数相等的A、B、C三个班，小聪、小慧都选择了“神奇魔方”．已知小聪不在A班，用列表法或画树状图法，求小聪和小慧被分到同一个班的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

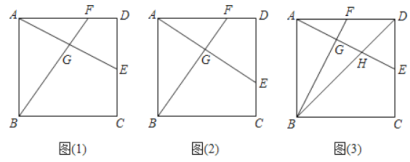
    【题目】如图，正方形的边长为分别是边上的动点，和交于点．

    如图(1)，若为边的中点，， 求的长；

    如图(2)，若点在上从向运动，点在．上从向运动．两点同时出发，同时到达各自终点，求在运动过程中，点运动的路径长：

    如图(3)， 若分别是边上的中点，与交于点，求的正切值．

    查看答案和解析>>

    同步练习册答案