
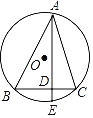
【题目】如图,⊙O是△ABC的外接圆,∠BAC=45°,AD⊥BC于点D,延长AD交⊙O于点E,若BD=4,CD=1,则DE的长是_____.
 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】如图,由两个长为2,宽为1的长方形组成“7”字图形.
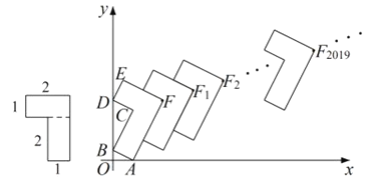
(1)将一个“7”字图形按如图摆放在平面直角坐标系中,记为“7”字图形![]() ,其中顶点
,其中顶点![]() 位于
位于![]() 轴上,顶点
轴上,顶点![]() ,
,![]() 位于
位于![]() 轴上,
轴上,![]() 为坐标原点,则
为坐标原点,则![]() 的值为____.
的值为____.
(2)在(1)的基础上,继续摆放第二个“7”字图形得顶点![]() ,摆放第三个“7”字图形得顶点
,摆放第三个“7”字图形得顶点![]() ,依此类推,…,摆放第
,依此类推,…,摆放第![]() 个“7”字图形得顶点
个“7”字图形得顶点![]() ,…,则顶点
,…,则顶点![]() 的坐标为_____.
的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
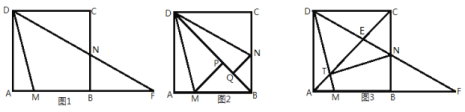
【题目】如图,在正方形ABCD中,点M、N分别在AB、BC边上,∠MDN=45°.
(1)如图1,DN交AB的延长线于点F. 求证:![]() ;
;
(2)如图2,过点M作MP⊥DB于P,过N作NQ⊥BD于![]() ,若
,若![]() ,求对角线BD的长;
,求对角线BD的长;
(3)如图3,若对角线AC交DM,DF分别于点T,E.判断△DTN的形状并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
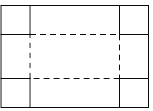
【题目】如图,把一块长为40cm,宽为30cm的矩形硬纸板的四角剪去四个相同小正方形,然后把纸板的四边沿虚线折起,并用胶带粘好,即可做成一个无盖纸盒.若该无盖纸盒的底面积为600cm2,设剪去小正方形的边长为xcm,则可列方程为( )
A.(30﹣2x)(40﹣x)=600B.(30﹣x)(40﹣x)=600
C.(30﹣x)(40﹣2x)=600D.(30﹣2x)(40﹣2x)=600
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为4的正方形ABCD中,点E为对角线AC上一动点(点E与点A,C不重合),连接DE,作EF⊥DE交射线BA于点F,过点E作MN∥BC分别交CD,AB于点M、N,作射线DF交射线CA于点G.
(1)求证:EF=DE;
(2)当AF=2时,求GE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,设二次函数y1=x2+bx+a,y2=ax2+bx+1(a,b是实数,a≠0).
(1)若函数y1的对称轴为直线x=3,且函数y1的图象经过点(a,b),求函数y1的表达式.
(2)若函数y1的图象经过点(r,0),其中r≠0,求证:函数y2的图象经过点(![]() ,0).
,0).
(3)设函数y1和函数y2的最小值分别为m和n,若m+n=0,求m,n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角边长为1的等腰直角三角形与边长为2的正方形在同一水平线上,三角形沿水平线从左向右匀速穿过正方形.设穿过时间为t,正方形与三角形不重合部分的面积为s(阴影部分),则s与t的大致图象为( )
![]()
A.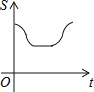 B.
B.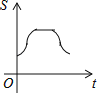
C.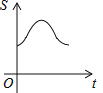 D.
D.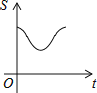
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() ,交
,交![]() 轴于
轴于![]() ,直线
,直线![]() 平行于
平行于![]() 轴,与抛物线另一个交点为
轴,与抛物线另一个交点为![]() .
.
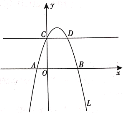
(1)求抛物线![]() 的函数表达式及点D的坐标;
的函数表达式及点D的坐标;
(2)若抛物线![]() 与抛物线
与抛物线![]() 关于
关于![]() 轴对称,
轴对称,![]() 是
是![]() 轴上的动点,在抛物线
轴上的动点,在抛物线![]() 上是否存在一点
上是否存在一点![]() ,使得以
,使得以![]() 为顶点且
为顶点且![]() 为边的四边形是平行四边形,若存在,请求出点
为边的四边形是平行四边形,若存在,请求出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com