
【题目】如图,在四边形ABCD中,∠A=∠C=90°,DE,BF分别平分∠ADC,∠ABC,并交线段AB,CD于点E,F(点E,B不重合).在线段BF上取点M,N(点M在BN之间),使BM=2FN.当点P从点D匀速运动到点E时,点Q恰好从点M匀速运动到点N.记QN=x,PD=y,已知![]() ,当Q为BF中点时,
,当Q为BF中点时,![]() .
.
(1)判断DE与BF的位置关系,并说明理由;
(2)求DE,BF的长;
(3)若AD=6.①当DP=DF时,通过计算比较BE与BQ的大小关系;②连结PQ,当PQ所在直线经过四边形ABCD的一个顶点时,求所有满足条件的x的值.

【答案】(1)![]() ,理由见解析;(2)
,理由见解析;(2)![]() ;(3)①
;(3)①![]() ;②
;②![]()
【解析】
(1)推出∠AED=∠ABF,即可得出DE∥BF;
(2)求出DE=12,MN=10,把![]() 代入
代入![]() ,解得:x=6,得到NQ=6,得出QM=4,由FQ=QB,BM=2FN,得出FN=2,BM=4,即可得出结果;
,解得:x=6,得到NQ=6,得出QM=4,由FQ=QB,BM=2FN,得出FN=2,BM=4,即可得出结果;
(3)①连接EM并延长交BC于点H,易证四边形DFME是平行四边形,得出DF=EM,求出∠DEA=∠FBE=∠FBC=30°,∠ADE=∠CDE=∠FME=60°,∠MEB=∠FBE=30°,得出∠EHB=90°,DF=EM=BM=4,MH=2,EH=6,由勾股定理得![]() ,
,![]() ,当DP=DF时 ,求出
,当DP=DF时 ,求出![]() ,得到BQ>BE;
,得到BQ>BE;
②(Ⅰ)当PQ经过点D时,y=0,则x=10;
(Ⅱ)当PQ经过点C时,由FQ∥DP,得出△CFQ∽△CDP,则![]() ,即可求得
,即可求得![]() ;
;
(Ⅲ)当PQ经过点A时,由PE∥BQ,得出△APE∽△AQB,则![]() ,根据勾股定理得
,根据勾股定理得![]() ,则
,则![]() ,
,![]() ;由图可知,PQ不可能过点B.
;由图可知,PQ不可能过点B.
解:(1)DE与BF的位置关系为:DE∥BF,理由如下:
如图1所示:
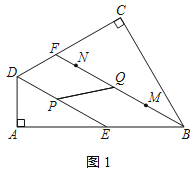
∵∠A=∠C=90°,
∴∠ADC+∠ABC=360°-(∠A+∠C)=180°,
∵DE、BF分别平分∠ADC、∠ABC,
![]()
![]()
∵∠ADE+∠AED=90°,
∴∠AED=∠ABF,
∴DE∥BF;
(2)令x=0,得y=12,
∴DE=12,
令y=0,得x=10,
∴MN=10,
把![]() 代入
代入![]() ,
,
解得:x=6,即NQ=6,
∴QM=10-6=4,
∵Q是BF中点,
∴FQ=QB,
∵BM=2FN,
∴FN+6=4+2FN,
解得:FN=2,
∴BM=4,
∴BF=FN+MN+MB=16;
(3)①连接EM并延长交BC于点H,如图2所示:
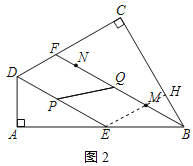
∵FM=2+10=12=DE,DE∥BF,
∴四边形DFME是平行四边形,
∴DF=EM,
∵AD=6,DE=12,∠A=90°,
∴∠DEA=30°,
∴∠DEA=∠FBE=∠FBC=30°,
∴∠ADE=60°,
∴∠ADE=∠CDE=∠FME=60°,
∴∠DFM=∠DEM=120°,
∴∠MEB=180°-120°-30°=30°,
∴∠MEB=∠FBE=30°,
∴∠EHB=180°-30°-30°-30°=90°,DF=EM=BM=4,
![]() ,
,
∴EH=4+2=6,
由勾股定理得:![]() ,
,
∴![]() ,
,
当DP=DF时,![]() ,
,
解得:![]() ,
,
![]() ,
,
![]() ,
,
BQ>BE;
②(Ⅰ)当PQ经过点D时,如图3所示:
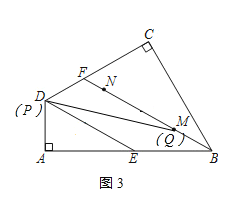
y=0,则x=10;
(Ⅱ)当PQ经过点C时,如图4所示:

∵BF=16,∠FCB=90°,∠CBF=30°,
![]() ,
,
CD=8+4=12,
∵FQ∥DP,
∴△CFQ∽△CDP,
∴![]() ,
,
∴ ,
,
解得:![]() ;
;
(Ⅲ)当PQ经过点A时,如图5所示:
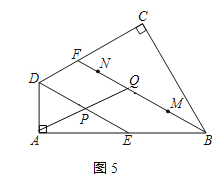
∵PE∥BQ,
∴△APE∽△AQB,
∴![]() ,
,
根据勾股定理得:![]() ,
,
∴![]() ,
,
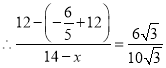 ,
,
解得:![]() ;
;
由图可知,PQ不可能过点B;
综上所述,当x=10或![]() 或
或![]() 时,PQ所在的直线经过四边形ABCD的一个顶点.
时,PQ所在的直线经过四边形ABCD的一个顶点.


科目:初中数学 来源: 题型:
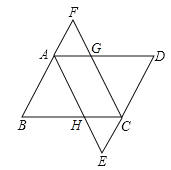
【题目】如图,四边形ABCD为平行四边形,∠BAD和∠BCD的平分线AE,CF分别交DC,BA的延长线于点E,F,交边BC,AD于点H,G.
(1)求证:四边形AECF是平行四边形.
(2)若AB=5,BC=8,求AF+AG的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
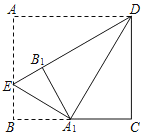
【题目】如图,在矩形ABCD中,AD=4,将∠A向内翻析,点A落在BC上,记为A1,折痕为DE.若将∠B沿EA1向内翻折,点B恰好落在DE上,记为B1,则AB=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
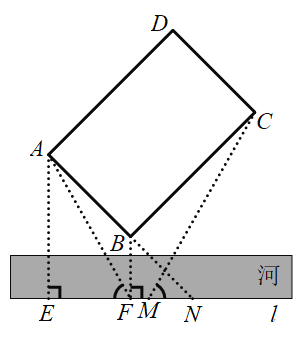
【题目】如图,在河对岸有一矩形场地ABCD,为了估测场地大小,在笔直的河岸l上依次取点E,F,N,使AE⊥l,BF⊥l,点N,A,B在同一直线上.在F点观测A点后,沿FN方向走到M点,观测C点发现∠1=∠2.测得EF=15米,FM=2米,MN=8米,∠ANE=45°,则场地的边AB为_______米,BC为_______米.
查看答案和解析>>
科目:初中数学 来源: 题型:
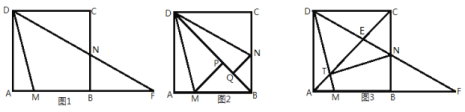
【题目】如图,在正方形ABCD中,点M、N分别在AB、BC边上,∠MDN=45°.
(1)如图1,DN交AB的延长线于点F. 求证:![]() ;
;
(2)如图2,过点M作MP⊥DB于P,过N作NQ⊥BD于![]() ,若
,若![]() ,求对角线BD的长;
,求对角线BD的长;
(3)如图3,若对角线AC交DM,DF分别于点T,E.判断△DTN的形状并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一块长为40cm,宽为30cm的矩形硬纸板的四角剪去四个相同小正方形,然后把纸板的四边沿虚线折起,并用胶带粘好,即可做成一个无盖纸盒.若该无盖纸盒的底面积为600cm2,设剪去小正方形的边长为xcm,则可列方程为( )
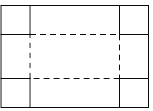
A.(30﹣2x)(40﹣x)=600B.(30﹣x)(40﹣x)=600
C.(30﹣x)(40﹣2x)=600D.(30﹣2x)(40﹣2x)=600
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,设二次函数y1=x2+bx+a,y2=ax2+bx+1(a,b是实数,a≠0).
(1)若函数y1的对称轴为直线x=3,且函数y1的图象经过点(a,b),求函数y1的表达式.
(2)若函数y1的图象经过点(r,0),其中r≠0,求证:函数y2的图象经过点(![]() ,0).
,0).
(3)设函数y1和函数y2的最小值分别为m和n,若m+n=0,求m,n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
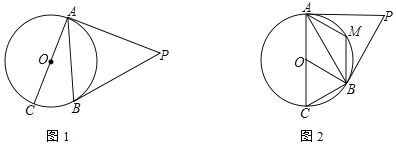
【题目】如图,AC是⊙O的直径,PA、PB是⊙O的切线,切点分别是点A、B
(1)如图1,若∠BAC=25°,求∠P的度数.
(2)如图2,若M是劣弧AB上一点,∠AMB=∠AOB,求∠P的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com