
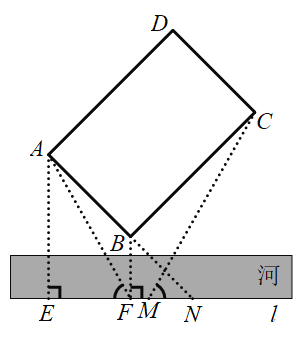
【题目】如图,在河对岸有一矩形场地ABCD,为了估测场地大小,在笔直的河岸l上依次取点E,F,N,使AE⊥l,BF⊥l,点N,A,B在同一直线上.在F点观测A点后,沿FN方向走到M点,观测C点发现∠1=∠2.测得EF=15米,FM=2米,MN=8米,∠ANE=45°,则场地的边AB为_______米,BC为_______米.
【答案】![]()
![]()
【解析】
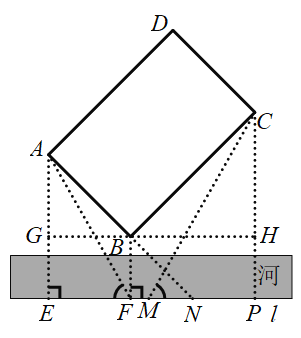
过点C作CP⊥EF于点P,过点B作直线GH∥EF交AE于点G,交CP于点H,如图,则△ABG、△BCH都是等腰直角三角形,四边形BGEF、BHPF是矩形,于是可根据等腰直角三角形的性质和勾股定理依次求出AG、BG、AB的长,设FP=BH=CH=x,则MP=x-2,CP=x+10,易证△AEF∽△CPM,然后根据相似三角形的性质即可得到关于x的方程,解方程即可求出x,再根据勾股定理即可求出BC的长.
解:过点C作CP⊥EF于点P,过点B作直线GH∥EF交AE于点G,交CP于点H,如图,则GH⊥AE,GH⊥CP,
∴四边形BGEF、BHPF是矩形,
∵∠ANE=45°,∴∠NAE=45°,
∴AE=EN=EF+FM+MN=15+2+8=25,
∵∠ABG=45°,∴∠GAB=45°,
∴AG=BG=EF=15,
∴![]() ,GE=BF=PH=10,
,GE=BF=PH=10,
∵∠ABG=45°,∠ABC=90°,∴∠CBH=45°,
∴∠BCH=45°,∴BH=CH,
设FP=BH=CH=x,则MP=x-2,CP=x+10,
∵∠1=∠2,∠AEF=∠CPM=90°,
∴△AEF∽△CPM,
∴![]() ,即
,即![]() ,解得:x=20,
,解得:x=20,
即BH=CH=20,
∴![]() .
.
∴![]() 米,
米,![]() 米.
米.
故答案为:![]() ,
,![]() .
.


科目:初中数学 来源: 题型:
【题目】“六一”儿童节前,玩具商店根据市场调查,用2500元购进一批儿童玩具,上市后很快脱销,接着又用4500元购进第二批这种玩具,所购数量是第一批数量的1.5倍,但每套进价多了10元.第一、二批玩具每套的进价分别是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两商场以同样的价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购物超过100元后,超出100元的部分按八折收费;在乙商场累计购物超过50元后,超出50元的部分按九折收费.设顾客累计购物![]() (单位:元),购物花费为
(单位:元),购物花费为![]() (单位:元).
(单位:元).
(1)分别写出在甲、乙两个商场购物时,![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)顾客到哪家商场购物花费少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲楼AB高20米,乙楼CD高10米,两栋楼之间的水平距离BD=30m,为了测量某电视塔EF的高度,小明在甲楼楼顶A处观测电视塔塔顶E,测得仰角为37°,小明在乙楼楼顶C处观测电视塔塔顶E,测得仰角为45°,求该电视塔的高度EF.
(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
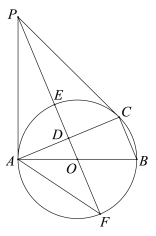
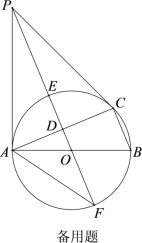
【题目】如图,⊙O是△ABC的外接圆,AB是直径,D是AC中点,直线OD与⊙O相交于E,F两点,P是⊙O外一点,P在直线OD上,连接PA,PC,AF,且满足∠PCA=∠ABC.
(1)求证:PA是⊙O的切线;
(2)证明:![]() ;
;
(3)若BC=8,tan∠AFP=![]() ,求DE的长.
,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠A=∠C=90°,DE,BF分别平分∠ADC,∠ABC,并交线段AB,CD于点E,F(点E,B不重合).在线段BF上取点M,N(点M在BN之间),使BM=2FN.当点P从点D匀速运动到点E时,点Q恰好从点M匀速运动到点N.记QN=x,PD=y,已知![]() ,当Q为BF中点时,
,当Q为BF中点时,![]() .
.
(1)判断DE与BF的位置关系,并说明理由;
(2)求DE,BF的长;
(3)若AD=6.①当DP=DF时,通过计算比较BE与BQ的大小关系;②连结PQ,当PQ所在直线经过四边形ABCD的一个顶点时,求所有满足条件的x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小寇随机调查了若干租用共享单车市民的骑车时间t(单位:分),将获得的据分成四组(A:0<t≤10,B:10<t≤20,C:20<t≤30, D:t>30),绘制了如下统计图,根据图中信息,解答下列问题:
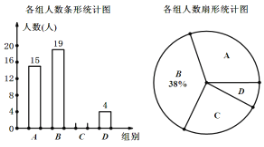
(1)小寇调查的总人数是 人;
(2)表示C组的扇形统计图的圆心角的度数是 °;
(3)如果小寇想从D组的甲、乙、丙、丁四人中随机选择两人进一步了解平时租用共享单车情况,请用列表或画树状图的方法求出丁被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知函数y1=x2+ax+1,y2=x2+bx+2,y3=x2+cx+4,其中a,b,c是正实数,且满足b2=ac.设函数y1,y2,y3的图象与x轴的交点个数分别为M1,M2,M3,( )
A.若M1=2,M2=2,则M3=0B.若M1=1,M2=0,则M3=0
C.若M1=0,M2=2,则M3=0D.若M1=0,M2=0,则M3=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y1=mx2+4mx﹣5m(m≠0),一次函数y2=2x﹣2,有下列结论:
①当x>﹣2时,y随x的增大而减小;
②二次函数y1=mx2+4mx﹣5m(m≠0)的图象与x轴交点的坐标为(﹣5,0)和(1,0);
③当m=1时,y1≤y2;
④在实数范围内,对于x的同一个值,这两个函数所对应的函数值y2≤y1均成立,则m![]() .
.
其中,正确结论的个数是( )
A.0B.1C.2D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com