
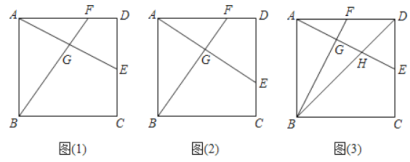
【题目】如图,正方形![]() 的边长为
的边长为![]() 分别是边
分别是边![]() 上的动点,
上的动点,![]() 和
和![]() 交于点
交于点![]() .
.
![]() 如图(1),若
如图(1),若![]() 为边
为边![]() 的中点,
的中点,![]() , 求
, 求![]() 的长;
的长;
![]() 如图(2),若点
如图(2),若点![]() 在
在![]() 上从
上从![]() 向
向![]() 运动,点
运动,点![]() 在
在![]() .上从
.上从![]() 向
向![]() 运动.两点同时出发,同时到达各自终点,求在运动过程中,点
运动.两点同时出发,同时到达各自终点,求在运动过程中,点![]() 运动的路径长:
运动的路径长:
![]() 如图(3), 若
如图(3), 若![]() 分别是边
分别是边![]() 上的中点,
上的中点,![]() 与
与![]() 交于点
交于点![]() ,求
,求![]() 的正切值.
的正切值.
【答案】![]() ;
;![]() ;
;![]()
【解析】
(1)延长BF、CD交于点H,根据勾股定理求出AE,证明△AFB∽△DFH,根据相似三角形的性质求出DH,再证明△AGB∽△EGH,最后根据相似三角形的性质计算即可;
(2)取AB的中点O,连接OG,证明△BAF≌△ADE,再确定∠AGB=90°,再根据直角三角形的性质求出OG,最后运用弧长公式计算即可;
(3)作FQ⊥BD于Q,设正方形的边长为2a,再用a表示出BQ、FQ,最后根据正切的定义即可解答.
解:(1)如图,延长BF、CD交于点H
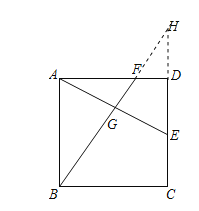
∵E为边CD的中点
∴DE=DC=3
由勾股定理可得![]() ,
,
∵四边形ABCD为正方形
∴AB∥CD
∴△AFB∽△DFH
∴![]()
∵AB=6,
∴DH=3,EH=6
∵AB//CD
∴△AGB∽△EGH,
∴![]()
∴![]() ;
;
(2)如图:

取AB的中点O,连接OG,
由题意可得,AF=DE
在△BAF和△ADE中
BA=AD, ∠BAF=∠ADE,AF=DE
∴△BAF≌△ADE(SAS)
∴∠ABF= ∠DAE
∵∠BAG+ ∠DAE=90°
∴∠BAG+ ∠ABG=90°,即∠AGB=90°
∵点O是AB的中点,
∴OG=![]() AB=3
AB=3
当点E与点C重合、点F与得D重合时,∠AOG=90°
∴点G运动的路径长为:![]() ;
;
(3)如图,作FQ⊥BD于Q,设正方形的边长为2a

∵点F是边AD上的中点
∴AF=DF=a,
∵四边形ABCD为正方形
∴![]() ,∠ADB=45°
,∠ADB=45°
∴![]()
∴![]()
∴ .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,把一块长为40cm,宽为30cm的矩形硬纸板的四角剪去四个相同小正方形,然后把纸板的四边沿虚线折起,并用胶带粘好,即可做成一个无盖纸盒.若该无盖纸盒的底面积为600cm2,设剪去小正方形的边长为xcm,则可列方程为( )
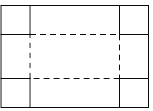
A.(30﹣2x)(40﹣x)=600B.(30﹣x)(40﹣x)=600
C.(30﹣x)(40﹣2x)=600D.(30﹣2x)(40﹣2x)=600
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点C、A分别在x轴、y轴上,AB∥x轴,∠ACB=90°,反比例函数y=![]() (x>0)的图象经过AB的中点M.若点A(0,4)、C(2,0),则k的值为( )
(x>0)的图象经过AB的中点M.若点A(0,4)、C(2,0),则k的值为( )
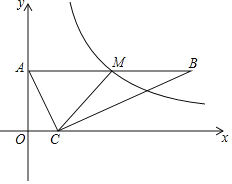
A.16B.20C.32D.40
查看答案和解析>>
科目:初中数学 来源: 题型:
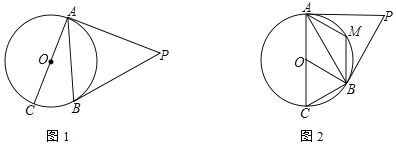
【题目】如图,AC是⊙O的直径,PA、PB是⊙O的切线,切点分别是点A、B
(1)如图1,若∠BAC=25°,求∠P的度数.
(2)如图2,若M是劣弧AB上一点,∠AMB=∠AOB,求∠P的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列各式规律:① 52-22=3×7;②72-42=3×11;③ 92-62=3×11;…;根据上面等式的规律:
(1)写出第6个和第n个等式;
(2)证明你写的第n个等式的正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() ,交
,交![]() 轴于
轴于![]() ,直线
,直线![]() 平行于
平行于![]() 轴,与抛物线另一个交点为
轴,与抛物线另一个交点为![]() .
.
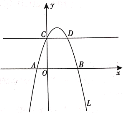
(1)求抛物线![]() 的函数表达式及点D的坐标;
的函数表达式及点D的坐标;
(2)若抛物线![]() 与抛物线
与抛物线![]() 关于
关于![]() 轴对称,
轴对称,![]() 是
是![]() 轴上的动点,在抛物线
轴上的动点,在抛物线![]() 上是否存在一点
上是否存在一点![]() ,使得以
,使得以![]() 为顶点且
为顶点且![]() 为边的四边形是平行四边形,若存在,请求出点
为边的四边形是平行四边形,若存在,请求出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
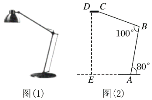
【题目】如图(1)是小明家购买的一款台灯,现忽略支架的粗细,得到它的侧面简化示意图如图(2)所示.支架AB与桌面的夹角为80°,支架AB与支架BC的夹角为100°,CD平行于桌面,支架AB,BC的长度均为20cm.求灯泡顶端D到桌面的距离DE.(结果精确到1cm.参考数据:sin80°≈0.98,cos80°≈0.17,tan80°≈5.67,sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
查看答案和解析>>
科目:初中数学 来源: 题型:
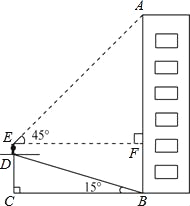
【题目】小华为了测量楼房AB的高度,他从楼底的B处沿着斜坡向上行走20m,到达坡顶D处.已知斜坡的坡角为15°.小华的身高ED是1.6m,他站在坡顶看楼顶A处的仰角为45°,求楼房AB的高度.(计算结果精确到1m)(参考数据:sin15°=![]() ,cos15°=
,cos15°=![]() ,tan15°=
,tan15°=![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com