
��ͼ����һ������ֽ�ϻ���һ����BAC���ҡ�BAC=����


��1����ͼ2����ֽƬ��BAC��DE����DEΪ�ۺۣ���ʹ����A�ڡ�BAC���ڲ�����A�ĶԳƵ�Ϊ��O����֤����CDO+��OEB=2����
��2����ͼ3����ֽƬ��BAC��DE����DEΪ�ۺۣ���ʹ����A�ڡ�BAC���ⲿ����A�ĶԳƵ�Ϊ��Oд����CDO����OEB����ĵ�ʽ��ϵ��ֻд���𰸣�����֤������
��3����ͼ4����ͼ2�Ļ���������FGΪ�ۺ۵�ֽƬ��ʹ����D��E�ڡ�BAC���ڲ����ҵ�D��E�ĶԳƵ�ֱ�Ϊ��P��Q�����CFP+��PMO+��ONQ+��QGB�Ĵ�С��
��4����ͼ5����һ���ࡰM����HUKL����֪����HIJ+��JKL=2��IJK���ֱ��ӳ�HI��LK���ڵ�R���ʡ�HRL���IJK�Ƿ���ȣ������ȣ�����֤�����������ȣ���˵�����ɣ���һ��������
�����㡿���α任�ۺ��⣮
����������1����ƽ�ǺͶ��۵����ʼ����CDO=180�㩁2��ADE���ɣ�
��2����ƽ�ǺͶ��۵����ʼ����OEB=��AED��180�㼴�ɣ�
��3���ɶ��ۺ�ƽ�ǵ�������мļ��㣬
��3�����ü���ͼ�Σ����ۣ�ƽ�ǵ�����ļ��㣮
����𡿽⣺��1������ͼ2��
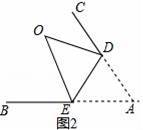

�߰�������ֽƬABC�ġ�A��DE���𣬵�A�ĶԳƵ�Ϊ��O��
���CDO+��OEB
=��180�㩁2��ADE��+��180�㩁2��AED��
=2��180�㩁��ADE����AED��=2����
��2����CDO����OEB=2����
�������£���ͼ3��


��CD0����OEB
=��180�㩁2��ADE������2��AED��180�㣩
=2��180�㩁��ADE����AED��
=2����
��3����CFP+PMO+��ONQ+��QGB=4����
�������£���ͼ4��
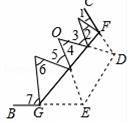

��CFP+��PMO+��ONQ+��QGB
=����CFP+��PMO��+����ONQ+QGB��
=2��FDM+2��NEG
=2����FDM+NEG��
=4��BAC
=4����
��4����HRL=��IJK��
�������£���ͼ5��


�ߡ�HIJ+��JKL
=����IRJ+��IJR��+����KRJ+��KJR��
=����IJR+��KJR��+����IRJ+��KRJ��
=��IJK+��IRK
=2��IJK��
���HRL=��IJK��
�������������Ǽ��α任�⣬��Ҫ�����˶��۵����ʣ�����Ĺؼ��ǴӸ���ͼ�η�������õIJ��֣������׳����ĵط��ǣ�д���ǣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����ͼ��ʾ������ϵ�£�
��1���������� ��ͼ������ͼ�����������⣺
��ͼ������ͼ�����������⣺
��2������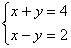 ��
��
��3������ʽ

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�Ĵ��Ű����������ֺ���ij��ѧ�ţ�1����ѧ����������װ��ģ���ͼ��ʾ�Ǹð�50��ѧ���ľ�����ͳ�ƣ������Ǿ�������������λ���ֱ��� .

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�Ӽף��ң�����������������ͬһ�ֲ�Ʒ�У������8����Ʒ����ʹ����������λ���꣩���и��ٵ��飬������£�
�ף�3��4��5��6��8��8��8��10��
�ң�4��6��6��6��8��9��12��14��
����3��3��3��7��9��10��10��11��
���������ڹ���ж��Ʋ�Ʒ��ʹ��������8�꣬����ݵ������жϳ����ڹ���зֱ�����ƽ��������������λ���е���һ�ּ������Ƶ�����������������Ϊ���� �ߣ����������õĽǶȻ�ѡ�����ֲ�Ʒ��
�ߣ����������õĽǶȻ�ѡ�����ֲ�Ʒ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
ij�̳�Ϊ�˴�����������1000Ԫ��Ʒ�Ĺ˿ͻ�齱ȯһ�ţ��齱����������µĵ緭���ƣ�һ�ų齱ȯֻ����һ�λ�����9��������ѡ��һ�����ƣ����Ӧ�ķ�����ǽ�Ʒ�������������Զ��������λ�ã���
��1����һ�ų齱ȯ����һ̨����ȵĸ��ʣ�
��2�������ų齱ȯ�����ƣ������������д��һ���¼���ʹ����¼������ĸ�����
 ��
��
| 1 | 2 | 3 |
| 4 | 5 | 6 |
| 7 | 8 | 9 |
����������
| һ̨����� | һ̨������ | лл���� |
| лл���� | һ������ | һ��U�� |
| ���ŵ�ӰƱ | лл���� | һ������ |
�����Ʒ��森
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��������ˮ��ʵ��Ʒ������5���ƽ����λ����������£���λ����/���꣩��

�����㣬 =10��
=10�� =10���Ը����������ݹ���__________��ˮ��Ʒ�ֵIJ����Ƚ��ȶ���
=10���Ը����������ݹ���__________��ˮ��Ʒ�ֵIJ����Ƚ��ȶ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
˳�����Ӿ����ı��е�õ����ı���һ���ǣ���
A.������ B.���� C.���� D.ƽ���ı���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com