
【题目】探究题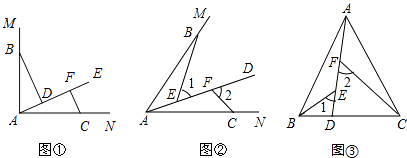
(1)理解证明:
如图1,∠MAN=90°,射线AE在这个角的内部,点B,C在∠MAN的边AM,AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.证明△ABD≌△CAF;
(2)类比探究:
如图2,点B,C在∠MAN的边AM、AN上,点E,F在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,∠1=∠2=∠BAC.求证:△ABE≌△CAF;
(3)如图3,在△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为15,则△ACF与△BDE的面积之和为多少?
【答案】
(1)
证明:∵CF⊥AE,BD⊥AE,
∴∠ADB=∠CFA=90°,
∵∠MAN=90°,
∴∠ABD+∠BAD=90°,又∠CAF+∠BAD=90°,
∴∠ABD=∠CAF,
在△ABD和△CAF中,
 ,
,
∴△ABD≌△CAF;
(2)
证明:∵∠1=∠2,
∴∠ABE=∠CAF,
∵∠1=∠ABE+∠EAB,∠1=∠BAC,
∴∠ABE=∠CAF,
在△ABE和△CAF中,
 ,
,
∴△ABE≌△CAF;
(3)
∵△ABC的面积为15,CD=2BD,
∴△ABD的面积为15× ![]() =5,
=5,
由类比探究得,△ABE≌△CAF,
∴△ACF与△BDE的面积之和=△ABD的面积=5
【解析】理解证明:根据AAS证明△ABD≌△CAF;
类比探究:根据AAS证明即可;
拓展应用:利用类比探究的结论、三角形的面积公式计算即可.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等三角形的对数是( )
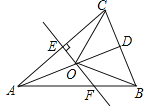
A.1对 B.2对 C.3对 D.4对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线MN是四边形AMBN的对称轴,点P是直线MN上的点,给出下列判断: ①AM=BM;②AP=BN;③∠MAP=∠MBP;④AN∥BP.其中结论正确的是:(填上序号即可)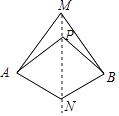
查看答案和解析>>
科目:初中数学 来源: 题型:
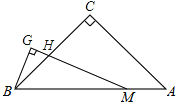
【题目】如图,△ABC中,∠C=90°,CA=CB,点M在线段AB上,∠GMB=![]() ∠A,BG⊥MG,垂足为G,MG与BC相交于点H.若MH=8cm,则BG= cm.
∠A,BG⊥MG,垂足为G,MG与BC相交于点H.若MH=8cm,则BG= cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边三角形ABC的边BC上任取一点D,以CD为边向外作等边三角形CDE(如图①),连接AD,BE,易证明BE=AD.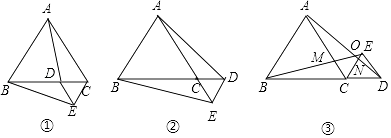
(1)若点D在射线BC上(如图②),其他条件均不变,BE=AD是否依然成立?试说明理由;
(2)在图②中,若等边三角形CDE与等边三角形ABC均在直线BC的同一侧(如图③),并且B,C,D三点在同一直线上,猜想BE=AD是否依然成立?试说明理由;
(3)在(2)的条件下,根据图汇总所标字母,请直接写出你发现的两个正确结论.
①;② .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据图回答下列问题![]()
(1)数轴上表示5与﹣2两点之间的距离是 ,
(2)数轴上表示x与2的两点之间的距离可以表示为 .
(3)如果|x﹣2|=5,则x= .
(4)同理|x+3|+|x﹣1|表示数轴上有理数x所对应的点到﹣3和1所对应的点的距离之和,请你找出所有符合条件的整数x,使得|x+3|+|x﹣1|=4,这样的整数是 .
(5)由以上探索猜想对于任何有理数x,|x﹣3|+|x﹣6|是否有最小值?如果有,直接写出最小值;如果没有,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八个边长为1的正方形如图摆放在平面直角坐标系中,经过P点的一条直线l将这八个正方形分成面积相等的两部分,则该直线l的解析式为( ) 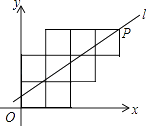
A.![]()
B.y= ![]() x+
x+ ![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com