
【题目】如图是一个正方体的表面展开图,如果正方体相对的面上标注的值相等,那么x+2y= . 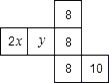
【答案】24
【解析】解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“2x”与“8”是相对面,
“y”与“10”是相对面,
∵正方体相对的面上标注的值相等,
∴2x=8,y=10,
∴x=4,
∴x+2y=4+2×10=24.
所以答案是:24.
【考点精析】利用解一元一次方程的步骤和几何体的展开图对题目进行判断即可得到答案,需要熟知先去分母再括号,移项变号要记牢.同类各项去合并,系数化“1”还没好.求得未知须检验,回代值等才算了;沿多面体的棱将多面体剪开成平面图形,若干个平面图形也可以围成一个多面体;同一个多面体沿不同的棱剪开,得到的平面展开图是不一样的,就是说:同一个立体图形可以有多种不同的展开图.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】探究题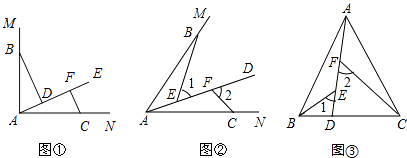
(1)理解证明:
如图1,∠MAN=90°,射线AE在这个角的内部,点B,C在∠MAN的边AM,AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.证明△ABD≌△CAF;
(2)类比探究:
如图2,点B,C在∠MAN的边AM、AN上,点E,F在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,∠1=∠2=∠BAC.求证:△ABE≌△CAF;
(3)如图3,在△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为15,则△ACF与△BDE的面积之和为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将△ABO绕点A顺指针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去…,若点A(![]() ,0),B(0,4),则点B2016的横坐标为( )
,0),B(0,4),则点B2016的横坐标为( )
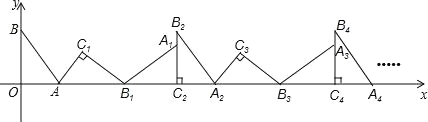
A.5 B.12 C.10070 D.10080
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等腰三角形的周长为20cm,将底边长y(cm)表示成腰长x(cm)的函数关系式是y=20-2x,则其自变量x的取值范围是( ).
A.0<x<10 B.5<x<10
C.一切实数 D.x>0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的四边相等,且面积为120cm2 , 对角线AC=24cm,则四边形ABCD的周长为( ) 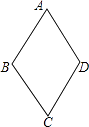
A.52cm
B.40cm
C.39cm
D.26cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八个边长为1的正方形如图摆放在平面直角坐标系中,经过P点的一条直线l将这八个正方形分成面积相等的两部分,则该直线l的解析式为( ) 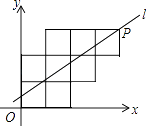
A.![]()
B.y= ![]() x+
x+ ![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
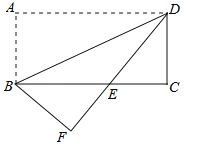
【题目】如图,将矩形纸片ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC于点E.
(1)求证:△DCE≌△BFE;
(2)若CD=2,∠ADB=30°,求BE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com