
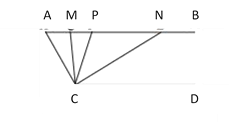
【题目】如图,已知AB∥CD,∠A=40°,点P是射线B上一动点(与点A不重合),CM,CN分别平分∠ACP和∠PCD,分别交射线AB于点M,N.
(1)求∠MCN的度数.
(2)当点P运动到某处时,∠AMC=∠ACN,求此时∠ACM的度数.
(3)在点P运动的过程中,∠APC与∠ANC的比值是否随之变化?若不变,请求出这个比值:若变化,请找出变化规律.
【答案】(1)∠MCN=70°;(2)∠ACM=35°;(3)不变.(详见解析)
【解析】
(1)由AB∥CD可得∠ACD=180°-∠A,再由CM、CN均为角平分线可求解;
(2)由AB∥CD可得∠AMC=∠MCD,再由∠AMC=∠ACN可得∠ACM =∠NCD;
(3)由AB∥CD可得∠APC=∠PCD,再由CN为角平分线即可解答.
解:(1)∵A B∥CD,
∴∠ACD=180°﹣∠A=140°,
又∵CM,CN分别平分∠ACP和∠PCD,
∴∠MCN=∠MCP+∠NCP=![]() (∠ACP+∠PCD)=
(∠ACP+∠PCD)=![]() ∠ACD=70°,
∠ACD=70°,
故答案为:70°.
(2)∵AB∥CD,
∴∠AMC=∠MCD,
又∵∠AMC=∠ACN,
∴∠MCD=∠ACN,
∴∠ACM=∠ACN﹣∠MCN=∠MCD﹣∠MCN=∠NCD,
∴∠ACM=∠MCP=∠NCP=∠NCD,
∴∠ACM=![]() ∠ACD=35°,
∠ACD=35°,
故答案为:35°.
(3)不变.理由如下:
∵AB∥CD,
∴∠APC=∠PCD,∠ANC=∠NCD,
又∵CN平分∠PCD,
∴∠ANC=∠NCD=![]() ∠PCD=
∠PCD=![]() ∠APC,即∠APC:∠ANC=2:1.
∠APC,即∠APC:∠ANC=2:1.


科目:初中数学 来源: 题型:
【题目】(1)计算并观察下列各式:
(x1)(x1) ;
(x1)( ![]() x1) ;
x1) ;
(x1)( ![]()
![]() x1) ;
x1) ;
(2)从上面的算式及计算结果,你发现了什么?请根据你发现的规律直接写下面的空格.(x1) ![]() 1;
1;
(3)利用你发现的规律计算:![]() ;
;
(4)利用该规律计算:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
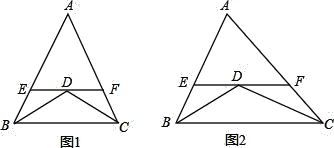
【题目】(1)如图1,已知:在△ABC中,AB=AC=10,BD平分∠ABC,CD平分∠ACB,过点D作EF∥BC,分别交AB、AC于E、F两点,则图中共有__________个等腰三角形;EF与BE、CF之间的数量关系是__________,△AEF的周长是__________;
(2)如图2,若将(1)中“△ABC中,AB=AC=10”该为“若△ABC为不等边三角形,AB=8,AC=10”其余条件不变,则图中共有__________个等腰三角形;EF与BE、CF之间的数量关系是什么?证明你的结论,并求出△AEF的周长;
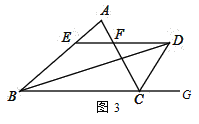
(3)已知:如图3,D在△ABC外,AB>AC,且BD平分∠ABC,CD平分△ABC的外角∠ACG,过点D作DE∥BC,分别交AB、AC于E、F两点,则EF与BE、CF之间又有何数量关系呢?直接写出结论不证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1+∠4﹦180°,∠2﹦∠E,则EF∥BC,下面是王华同学的推导过程﹐请你帮他在括号内填上推导依据或内容.
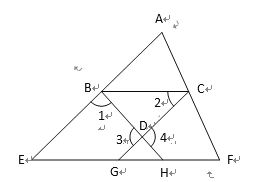
证明:
∵∠1+∠4﹦180°( ),
∠3﹦∠4 ( ),
∴∠1﹢ ﹦180°.
∴AE∥CG ( )
∴∠E﹦∠CGF( ).
∵∠2﹦∠E(已知)
∴ ∠2﹦∠CGF( ).
∴ BC∥EF( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 地某厂和
地某厂和![]() 地某厂同时制成机器若干台,
地某厂同时制成机器若干台,![]() 地某厂可支援外地
地某厂可支援外地![]() 台,
台,![]() 地某厂可支援外地
地某厂可支援外地![]() 台,现决定给
台,现决定给![]() 地
地![]() 台,
台,![]() 地
地![]() 台,已知从
台,已知从![]() 运往
运往![]() 、
、![]() 两地的运费分别是
两地的运费分别是![]() 元每台、
元每台、![]() 元每台,从
元每台,从![]() 运往
运往![]() 、
、![]() 两地的运费分别是
两地的运费分别是![]() 元每台、
元每台、![]() 元每台.
元每台.
(1)设![]() 地某厂运往
地某厂运往![]() 地
地![]() 台,求总运费为多少元?
台,求总运费为多少元?
(2)在(1)中,当![]() 时,总运费是多少元?
时,总运费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,我们定义点P(a ,b )的“伴随点”为Q,且规定:当a ≥ b时,Q为( b,-a );当 a<b 时,Q为( a,-b).
(1)点(2,1)的伴随点坐标为__________;
(2)若点A(a ,2)的伴随点在函数y=![]() 的图像上,求a的值;
的图像上,求a的值;
(3)已知直线l与坐标轴交于(6,0),(0,3)两点.将直线l上所有点的伴随点组成一个新的图形记作M.请直接写出直线y=—x+c与图形M有交点时相应的c的取值范围为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两个工程队承包了地铁某标段全长3900米的施工任务,分别从南,北两个方向同时向前掘进。已知甲工程队比乙工程队平均每天多掘进0.4米经过13天的施工两个工程队共掘进了156米.
(1)求甲,乙两个工程队平均每天各掘进多少米?
(2)为加快工程进度两工程队都改进了施工技术,在剩余的工程中,甲工程队平均每天能比原来多掘进0.4米,乙工程队平均每天能比原来多掘进0.6米,按此施工进度能够比原来少用多少天完成任务呢?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com