
【题目】(10分)如图,已知Rt△ABC中,∠C=90°,D为BC的中点,以AC为直径的⊙O交AB于点E.
(1)求证:DE是⊙O的切线;
(2)若AE:EB=1:2,BC=6,求⊙O的半径.

【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)求出∠OED=∠BCA=90°,根据切线的判定即可得出结论;
(2)求出△BEC∽△BCA,得出比例式,代入求出即可.
试题解析:(1)证明:连接OE、EC.

∵AC是⊙O的直径,∴∠AEC=∠BEC=90°.∵D为BC的中点,∴ED=DC=BD,∴∠1=∠2.∵OE=OC,∴∠3=∠4,∴∠1+∠3=∠2+∠4,即∠OED=∠ACB.
∵∠ACB=90°,∴∠OED=90°,∴DE是⊙O的切线;
(2)由(1)知:∠BEC=90°.在Rt△BEC与Rt△BCA中,∵∠B=∠B,∠BEC=∠BCA,∴△BEC∽△BCA,∴BE:BC=BC:BA,∴BC2=BEBA.∵AE:EB=1:2,设AE=x,则BE=2x,BA=3x.∵BC=6,∴62=2x3x,解得:x=![]() ,即AE=
,即AE=![]() ,∴AB=
,∴AB=![]() ,∴AC=
,∴AC=![]() =
=![]() ,∴⊙O的半径=
,∴⊙O的半径=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图1,2分别是某款篮球架的实物图与示意图,已知底座BC=0.60米,底座BC与支架AC所成的角∠ACB=75°,支架AF的长为2.50米,篮板顶端F点到篮框D的距离FD=1.35米,篮板底部支架HE与支架AF所成的角∠FHE=60°,求篮框D到地面的距离(精确到0.01米)(参考数据:cos75°≈0.2588,sin75°≈0.9659,tan75°≈3.732,![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,观察由棱长为 ![]() 的小立方体摆成的图形,寻找规律:如图 ① 中,共有
的小立方体摆成的图形,寻找规律:如图 ① 中,共有 ![]() 个小立方体,其中
个小立方体,其中 ![]() 个看得见,
个看得见, ![]() 个看不见;如图 ② 中,共有
个看不见;如图 ② 中,共有 ![]() 个小立方体,其中
个小立方体,其中 ![]() 个看得见,
个看得见, ![]() 个看不见;如图 ③ 中,共有
个看不见;如图 ③ 中,共有 ![]() 个小立方体,其中
个小立方体,其中 ![]() 个看得见,
个看得见, ![]() 个看不见;
个看不见; ![]() ,则第 ⑥个图中,看得见的小立方体有________________个.
,则第 ⑥个图中,看得见的小立方体有________________个.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上, 老师要求同学们利用三角板画两条平行线.老师说苗苗和小华两位同学画法都是正确的,两位同学的画法如下:
苗苗的画法:

①将含30°角的三角尺的最长边与直线a重合,另一块三角尺最长边与含30°角的三角尺的最短边紧贴;
②将含30°角的三角尺沿贴合边平移一段距离,画出最长边所在直线b,则b//a.
小华的画法:
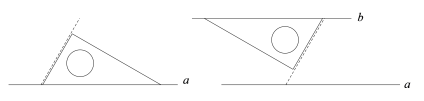
①将含30°角三角尺的最长边与直线a重合,用虚线做出一条最短边所在直线;
②再次将含30°角三角尺的最短边与虚线重合,画出最长边所在直线b,则b//a.
请在苗苗和小华两位同学画平行线的方法中选出你喜欢的一种,并写出这种画图的依据.
答:我喜欢__________同学的画法,画图的依据是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,∠ABC=60°,P是射线BD上一动点,以AP为边向右侧作等边△APE,连接CE.
(1)如图1,当点P在菱形ABCD内部时,则BP与CE的数量关系是 ,CE与AD的位置关系是 .
(2)如图2,当点P在菱形ABCD外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,请说明理由;
(3)如图2,连接BE,若AB=2![]() ,BE=2
,BE=2![]() ,求AP的长.
,求AP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读材料)
因式分解:![]() .
.
解:将“![]() ”看成整体,令
”看成整体,令![]() ,则原式
,则原式![]() .
.
再将“![]() ”还原,原式
”还原,原式![]() .
.
上述解题用到的是“整体思想”,整体思想是数学解题中常用的一种思想方法.
(问题解决)
(1)因式分解:![]() ;
;
(2)因式分解:![]() ;
;
(3)证明:若![]() 为正整数,则代数式
为正整数,则代数式![]() 的值一定是某个整数的平方.
的值一定是某个整数的平方.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二元一次方程组![]() 的解 x,y 的值是一个等腰三角形两边的长,且这个等腰三角形的周长为 5,求腰的长.(注:等腰三角形中相等的两条边叫做等腰三角形的腰)
的解 x,y 的值是一个等腰三角形两边的长,且这个等腰三角形的周长为 5,求腰的长.(注:等腰三角形中相等的两条边叫做等腰三角形的腰)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在纸面上有一数轴(如图),折叠纸面.
(1)若1表示的点与﹣1表示的点重合,则﹣2.5表示的点与数 表示的点重合;
(2)若﹣1表示的点与5表示的点重合,回答以下问题:
①5表示的点与数 表示的点重合;
②若数轴上A、B两点之间的距离为9(A在B的左侧),且A、B两点经折叠后重合,求A、B两点表示的数是多少?
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com