
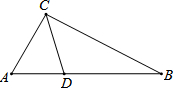
 交通对城市的发展发挥着十分重要的作用,如图,B市位于A市的正东方向,原来从A市到B市要经过C市,C市位于A市北偏东30°方向,位于B市北偏西53°方向,A到C的距离为150千米,现从A、B之间新修了一条直达的高速公路AB.
交通对城市的发展发挥着十分重要的作用,如图,B市位于A市的正东方向,原来从A市到B市要经过C市,C市位于A市北偏东30°方向,位于B市北偏西53°方向,A到C的距离为150千米,现从A、B之间新修了一条直达的高速公路AB.分析 (1)过C作CE⊥AB,根据题意知∠ACE=30°,∠ECB=53°,AC=150,解直角三角形即可求得AB长;
(2)作DF⊥AC于F,通过解直角三角形求解;即可得出AD的长.
解答 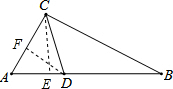 解:(1)作CE⊥AB于E,
解:(1)作CE⊥AB于E,
由题意可知,∠ACE=30°,∠ECB=53°,
在RT△ACE中,AC=150,
∴CE=$\frac{\sqrt{3}}{2}$AC=75$\sqrt{3}$,AE=$\frac{1}{2}$AC=75,
在RT△BCE中,EC=75$\sqrt{3}$,
∴BE=tan53°•CE=$\frac{4}{3}$×75$\sqrt{3}$=100$\sqrt{3}$,
∴AB=AE+BE=75+100$\sqrt{3}$(千米),
故新修高速公路AB的长度为(75+100$\sqrt{3}$)千米;
(2)作DF⊥AC于F,
∵∠ACE=30°,∠DCE=15°
∴∠ACD=45°,∠A=60°,
∴∠CDF=45°,
∴ACD=∠CDF,
∴CF=DF,
∴AF=$\frac{1}{2}$AD,CF=DF=$\frac{\sqrt{3}}{2}$AD,
∴$\frac{1}{2}$AD+$\frac{\sqrt{3}}{2}$AD=150,
∴AD=$150\sqrt{3}-150$.
所以,D到A市距离为(150$\sqrt{3}$-150)千米.
点评 本题考查的是解直角三角形的应用-方向角问题,根据题意作出辅助线,利用直角三角形的性质求解是解答此题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
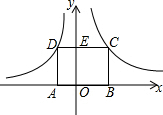 如图,矩形ABCD的顶点A在x轴负半轴上,点B在x轴正半轴,点C在反比例函数y=$\frac{4}{x}$第一象限的图象上,点D在反比例函数y=$\frac{k}{x}$的图象上,CD交y轴于点E.若DE:CE=1:2,则k的值是-2.
如图,矩形ABCD的顶点A在x轴负半轴上,点B在x轴正半轴,点C在反比例函数y=$\frac{4}{x}$第一象限的图象上,点D在反比例函数y=$\frac{k}{x}$的图象上,CD交y轴于点E.若DE:CE=1:2,则k的值是-2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
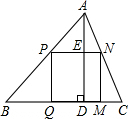 如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要把它加工成正方形零件PQMN,使正方形PQMN的边QM在BC上,其余两个项点P,N分别在AB,AC上.求这个正方形零件PQMN面积S.
如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要把它加工成正方形零件PQMN,使正方形PQMN的边QM在BC上,其余两个项点P,N分别在AB,AC上.求这个正方形零件PQMN面积S.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com