
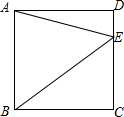
 如图,点E在正方形ABCD的边CD上,若△ABE的面积为18,CE=4,则线段BE的长为2$\sqrt{13}$.
如图,点E在正方形ABCD的边CD上,若△ABE的面积为18,CE=4,则线段BE的长为2$\sqrt{13}$.  学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 调查某品牌牛奶质量合格率 | |
| B. | 调查某幼儿园一班学生的平均身高 | |
| C. | 调查某市中小学生收看纪念抗日战争胜利70周年大阅兵的情况 | |
| D. | 调查某省九年级学生一周内网络自主学习的情况 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
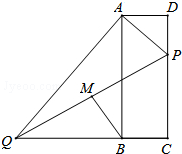 如图,在矩形ABCD中,点P在边CD上,且与C、D不重合,过点A作AP的垂线与CB的延长线相交于点Q,连接PQ,M为PQ中点.
如图,在矩形ABCD中,点P在边CD上,且与C、D不重合,过点A作AP的垂线与CB的延长线相交于点Q,连接PQ,M为PQ中点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
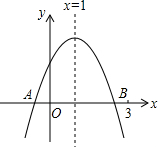 如图,二次函数y=ax2+bx+c的图象交x轴于A、B两点,下列结论:
如图,二次函数y=ax2+bx+c的图象交x轴于A、B两点,下列结论:| A. | 3个 | B. | 2个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2015}{2016}$ | B. | $\frac{2017}{2016}$ | C. | $\frac{2015}{2017}$ | D. | $\frac{2016}{2017}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (0,3) | B. | (-1,3) | C. | (3,-1) | D. | (3,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com