
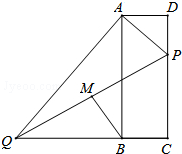
 如图,在矩形ABCD中,点P在边CD上,且与C、D不重合,过点A作AP的垂线与CB的延长线相交于点Q,连接PQ,M为PQ中点.
如图,在矩形ABCD中,点P在边CD上,且与C、D不重合,过点A作AP的垂线与CB的延长线相交于点Q,连接PQ,M为PQ中点.分析 (1)根据矩形的性质得出∠D=∠ABC=90°,∠DAB=90°,求出∠QAB=∠DAP,∠ABQ=∠D,根据相似三角形的判定得出即可;
(2)作MN⊥QC,根据相似三角形的判定得出△MQN∽△PQC,根据相似三角形的性质得出$\frac{MN}{PC}=\frac{QM}{QP}$,求出$\frac{MN}{PC}=\frac{QM}{QP}=\frac{QN}{QC}$=$\frac{1}{2}$,求出PC=20-x,MN=$\frac{1}{2}$(20-x),QN=$\frac{1}{2}$(QB+10),根据相似三角形的性质求出BQ,求出BN=x-5,根据勾股定理得出y=$\frac{5}{4}$x2-20x+125(0≤x≤20),化成顶点式,即可求出最值.
解答 (1)证明:∵四边形ABCD是矩形,
∴∠D=∠ABC=90°,∠DAB=90°,
∴∠ABQ=90°=∠D,
∵AQ⊥AP,
∴∠QAP=∠DAB=90°,
∴∠DAP=∠QAB=90°-∠BAP,
即∠QAB=∠DAP,∠ABQ=∠D,
∴△ADP∽△ABQ;
(2)解:作MN⊥QC,则∠QNM=∠QCD=90°,
又∵∠MQN=∠PQC
∴△MQN∽△PQC,
∴$\frac{MN}{PC}=\frac{QM}{QP}$,
∵∠C=∠MNQ=90°,
∴MN∥PC,
∵M为PQ的中点,
∴N为CQ的中点,
∴$\frac{MN}{PC}=\frac{QM}{QP}=\frac{QN}{QC}$=$\frac{1}{2}$,
又∵PC=DC-DP=20-x
∴MN=$\frac{1}{2}$PC=$\frac{1}{2}$(20-x),QN=$\frac{1}{2}$QC=$\frac{1}{2}$(QB+10),
∵△ADP∽△ABQ
∴$\frac{AD}{AB}$=$\frac{DP}{BQ}$,
∴$\frac{10}{20}$=$\frac{x}{BQ}$,
∴BQ=2x,
∵QN=$\frac{1}{2}$QC=$\frac{1}{2}$(QB+10)=$\frac{1}{2}$(2x+10)=x+5,
∴BN=QB-QN=2x-(x+5)=x-5,
在Rt△MBN中,由勾股定理得:BM2=MN2+BN2=[$\frac{1}{2}$(20-x)]2+(x-5)2,
即:y=$\frac{5}{4}$x2-20x+125,(0≤x≤20),
当x=8,即DP=8时,线段BM长的最小值=$\sqrt{45}$=3$\sqrt{5}$.
点评 本题考查了二次函数的最值,矩形的性质,相似三角形的性质和判定,勾股定理的应用,能综合运用定理进行推理和计算是解此题的关键,题目比较好,难度偏大.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{4}{9}$ | D. | $\frac{5}{9}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
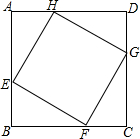 如图,正方形ABCD的边长为8cm,E、F、G、H分别是AB,BC,CD,DA上的动点,且AE=BF=CG=DH,
如图,正方形ABCD的边长为8cm,E、F、G、H分别是AB,BC,CD,DA上的动点,且AE=BF=CG=DH,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com