
【题目】(阅读理解)
我们将使得函数值为零的自变量的值称为函数的零点值,此时的点称为函数的零点.例如,对于函数y=x-1,令y=0,可得x=1,我们就说1是函数y=x-1的零点值,点(1,0)是函数y=x-1的零点.
(问题解决)
(1)已知函数![]() ,则它的零点坐标为________;
,则它的零点坐标为________;
(2)若二次函数y=x2-2x+m有两个零点,则实数m的取值范围是________;
(3)已知二次函数![]() 的两个零点都是整数点,求整数k的值.
的两个零点都是整数点,求整数k的值.
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,且AB为⊙O的直径.∠ACB的平分线交⊙O于点D,过点D作⊙O的切线PD交CA的延长线于点P,过点A作AE⊥CD于点E,过点B作BF⊥CD于点F.
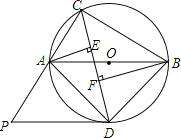
(1)求证:EF +AE= BF ;
(2)求证:△PDA∽△PCD ;
(3)若AC=6,BC=8,求线段PD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=![]() ,BC=1,将△ABD沿射线DB平移得到△A'B'D',连接B′C,D′C,则B'C+D'C的最小值是_____.
,BC=1,将△ABD沿射线DB平移得到△A'B'D',连接B′C,D′C,则B'C+D'C的最小值是_____.
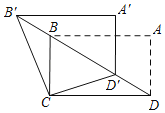
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有四张正面分别标有数字0,1,2,3的不透明卡片,它们除数字外其余全部相同,现将它们背面朝上洗均匀.
(1)随机抽出一张卡片,则抽到数字“2”的概率为 ;
(2)随机抽出一张卡片,记下数字后放回并搅匀,再随机抽出一张卡片,请用列表或画树状图的方法,求两次抽出的卡片上的数字之和是3的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
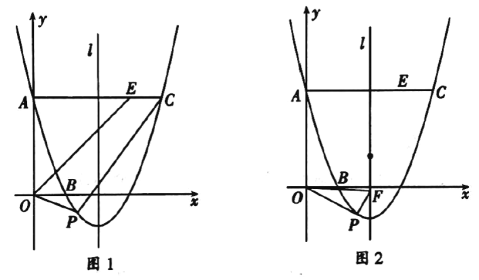
【题目】如图,已知抛物线![]() 的图像经过点
的图像经过点![]() ,
,![]() ,其对称轴为直线
,其对称轴为直线![]() :
:![]() ,过点
,过点![]() 作
作![]() 轴交抛物线于点
轴交抛物线于点![]() ,
,![]() 的平分线交线段
的平分线交线段![]() 于点
于点![]() ,点
,点![]() 是抛物线上的一个动点,设其横坐标为
是抛物线上的一个动点,设其横坐标为![]() .
.
(1)求抛物线的解析式;
(2)如图1,动点![]() 在直线
在直线![]() 下方的抛物线上,连结
下方的抛物线上,连结![]() ,当
,当![]() 为何值时,四边形
为何值时,四边形![]() 面积最大,并求出其最大值,
面积最大,并求出其最大值,
(3)如图②,![]() 是抛物线的对称轴
是抛物线的对称轴![]() 上的一点,连接
上的一点,连接![]() ,在抛物线
,在抛物线![]() 轴下方的图像上是否存在点
轴下方的图像上是否存在点![]() 使
使![]() 满足:①
满足:①![]() ;②
;②![]() ?若存在,求点
?若存在,求点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国的数字支付正在引领未来世界的支付方式变革.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
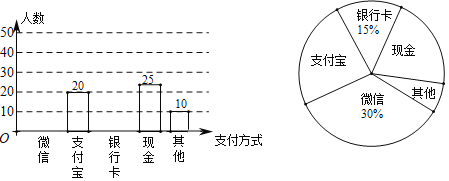
(1)这次活动共调查了 人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为 ;
(2)将条形统计图补充完整.观察此图,将各种支付方式调查人数组成一组数据,求这组数据的“中位数”是“ ”;
(3)在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表的方法,求两人选同种支付方式的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,动点P从点A出发,沿A→D→C→B的路径运动.设点P运动的路程为x,△PAB的面积为y.图2反映的是点P在A→D→C运动过程中,y与x的函数关系.请根据图象回答以下问题:
(1)矩形ABCD的边AD=________,AB=________;
(2)写出点P在C→B运动过程中y与x的函数关系式,并在图2中补全函数图象.
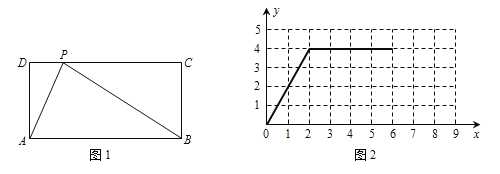
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 过点
过点![]() ,
, ![]() .
. ![]() 为线段OA上一个动点(点M与点A不重合),过点M作垂直于x轴的直线与直线AB和抛物线分别交于点P、N.
为线段OA上一个动点(点M与点A不重合),过点M作垂直于x轴的直线与直线AB和抛物线分别交于点P、N.
(1)求直线AB的解析式和抛物线的解析式;
(2)如果点P是MN的中点,那么求此时点N的坐标;
(3)如果以B,P,N为顶点的三角形与![]() 相似,求点M的坐标.
相似,求点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1为含锐角是30°的直角三角尺,其边框为透明塑料制成(内、外直角三角形对应边互相平行且三处所示宽度相等).将三角尺移向直径为4cm的⊙O,它的内Rt△ABC的斜边AB恰好等于⊙O的直径,它的外Rt△A′B′C′的直角边A′C′恰好与⊙O相切(如图2).
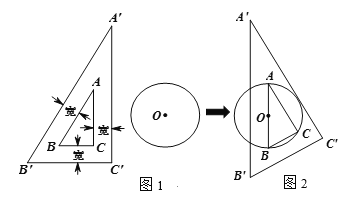
(1)求直角三角尺边框的宽;
(2)求边B′C′的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com