
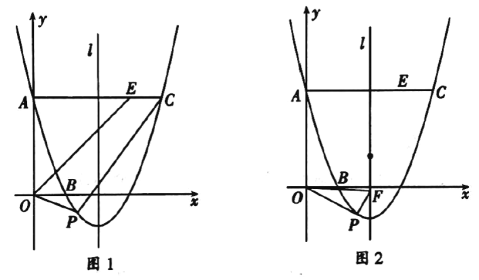
【题目】如图,已知抛物线![]() 的图像经过点
的图像经过点![]() ,
,![]() ,其对称轴为直线
,其对称轴为直线![]() :
:![]() ,过点
,过点![]() 作
作![]() 轴交抛物线于点
轴交抛物线于点![]() ,
,![]() 的平分线交线段
的平分线交线段![]() 于点
于点![]() ,点
,点![]() 是抛物线上的一个动点,设其横坐标为
是抛物线上的一个动点,设其横坐标为![]() .
.
(1)求抛物线的解析式;
(2)如图1,动点![]() 在直线
在直线![]() 下方的抛物线上,连结
下方的抛物线上,连结![]() ,当
,当![]() 为何值时,四边形
为何值时,四边形![]() 面积最大,并求出其最大值,
面积最大,并求出其最大值,
(3)如图②,![]() 是抛物线的对称轴
是抛物线的对称轴![]() 上的一点,连接
上的一点,连接![]() ,在抛物线
,在抛物线![]() 轴下方的图像上是否存在点
轴下方的图像上是否存在点![]() 使
使![]() 满足:①
满足:①![]() ;②
;②![]() ?若存在,求点
?若存在,求点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
【答案】(1)y=x2-4x+3;(2),当![]() =
=![]() 时,四边形
时,四边形![]() 面积最大,最大值是
面积最大,最大值是![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)首先根据对称性得出抛物线与![]() 轴的另一个交点坐标,然后根据两坐标设抛物线解析式,代入点A的坐标,即可得解;
轴的另一个交点坐标,然后根据两坐标设抛物线解析式,代入点A的坐标,即可得解;
(2)设P坐标,过点P作PF||![]() 轴,将四边形OPCE的面积表示为:
轴,将四边形OPCE的面积表示为:![]() ,计算即可;
,计算即可;
(3)区分为P在对称轴左,右两侧进行讨论,借用![]() ,构造一线三角形相似,列出等量关系,计算即可.
,构造一线三角形相似,列出等量关系,计算即可.
(1)如图,设抛物线与![]() 轴的另一个交点为D
轴的另一个交点为D
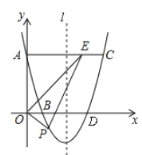
由对称性得:D(3,0)
设抛物线的解析式为:![]()
把A(0,3)代入得:![]() 即
即![]()
∴抛物线的解析式:![]()
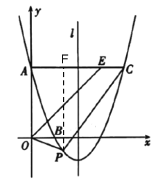
(2)如图,过点P作![]() 轴,交AC于点F
轴,交AC于点F
在![]() 中,点A与点C关于对称轴对称
中,点A与点C关于对称轴对称
∵A(0,3),∴C(4,3)
∵OE平分![]() ,且
,且![]()
∴![]()
∴AE=AO=3
设![]() ,则
,则![]()
则![]() ,
,![]() ,
,![]()
故![]()
![]()
![]()
![]()
∵P在BC的下方
∴![]()
∴当![]() 时,四边形OPCE的面积最大,最大值为:
时,四边形OPCE的面积最大,最大值为:![]()
(3)若点P在对称轴左侧,
过点P作![]() 交
交![]() 轴于点M,交
轴于点M,交![]() 于点N
于点N
由题得:![]()
∴![]()
∵![]() ,则
,则![]() ,
,![]() ,
,![]()
∴ ,解得
,解得![]()
此时![]()

若点P在对称轴右侧
过点P作![]() 交
交![]() 轴于点N,过点F作
轴于点N,过点F作![]() 交MN于点M
交MN于点M
由题得:![]()
∴![]()
∵![]() ,则
,则![]() ,
, ![]()
∴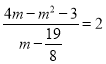 ,解得
,解得![]()
此时![]()
综上:点P为![]() ,
,![]() .
.


科目:初中数学 来源: 题型:
【题目】(概念认识)
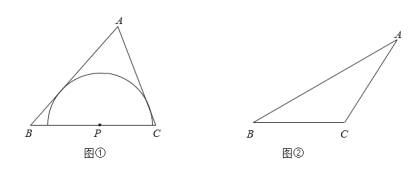
若以三角形某边上任意一点为圆心,所作的半圆上的所有点都在该三角形的内部或边上,则将符合条件且半径最大的半圆称为该边关联的极限内半圆.
如图①,点P是锐角△ABC的边BC上一点,以P为圆心的半圆上的所有点都在△ABC的内部或边上.当半径最大时,半圆P为边BC关联的极限内半圆.
(初步思考)
(1)若等边△ABC的边长为1,则边BC关联的极限内半圆的半径长为 .
(2)如图②,在钝角△ABC中,用直尺和圆规作出边BC关联的极限内半圆(保留作图痕迹,不写作法).
(深入研究)
(3)如图③,∠AOB=30°,点C在射线OB上,OC=6,点Q是射线OA上一动点.在△QOC中,若边OC关联的极限内半圆的半径为r,当1≤r≤2时,求OQ的长的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=x2﹣2x+k与x轴交于A、B两点,与y轴交于点C(0,﹣3).[图2、图3为解答备用图]
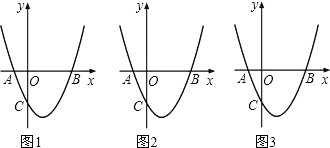
(1)k= ,点A的坐标为 ,点B的坐标为 ;
(2)设抛物线y=x2﹣2x+k的顶点为M,求四边形ABMC的面积;
(3)在x轴下方的抛物线上是否存在一点D,使四边形ABDC的面积最大?若存在,请求出点D的坐标;若不存在,请说明理由;
(4)在抛物线y=x2﹣2x+k上求点Q,使△BCQ是以BC为直角边的直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 经过点
经过点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
![]() 求这条抛物线的解析式;
求这条抛物线的解析式;
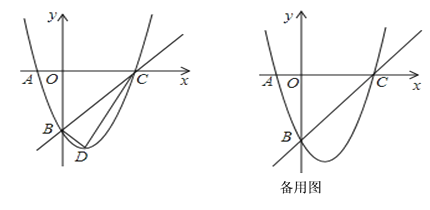
![]() 如图1,点P是第三象限内抛物线上的一个动点,当四边形
如图1,点P是第三象限内抛物线上的一个动点,当四边形![]() 的面积最大时,求点
的面积最大时,求点![]() 的坐标;
的坐标;
![]() 如图2,线段
如图2,线段![]() 的垂直平分线交
的垂直平分线交![]() 轴于点
轴于点![]() ,垂足为
,垂足为![]() 为抛物线的顶点,在直线
为抛物线的顶点,在直线![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 的周长最小?若存在,求出点
的周长最小?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店用4500元购进一批衬衫,很快售完,服装店老板又用2100元购进第二批该款式的衬衫,进货量是第一次的一半,但进价每件比第一批降低了10元.
(1)这两次各购进这种衬衫多少件?
(2)若第一批衬衫的售价是200元/件,老板想让这两批衬衫售完后的总利润不低于1950元,则第二批衬衫每件至少要售多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读理解)
我们将使得函数值为零的自变量的值称为函数的零点值,此时的点称为函数的零点.例如,对于函数y=x-1,令y=0,可得x=1,我们就说1是函数y=x-1的零点值,点(1,0)是函数y=x-1的零点.
(问题解决)
(1)已知函数![]() ,则它的零点坐标为________;
,则它的零点坐标为________;
(2)若二次函数y=x2-2x+m有两个零点,则实数m的取值范围是________;
(3)已知二次函数![]() 的两个零点都是整数点,求整数k的值.
的两个零点都是整数点,求整数k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“六一”儿童节前,玩具商店根据市场调查,用2500元购进一批儿童玩具,上市后很快脱销,接着又用4500元购进第二批这种玩具,所购数量是第一批数量的1.5倍,但每套进价多了10元.第一、二批玩具每套的进价分别是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,![]() 是一元二次方程
是一元二次方程![]() 的两个实数根,且
的两个实数根,且![]() ,抛物线
,抛物线![]() 的图象经过点
的图象经过点![]() ,
,![]() ,如图所示.
,如图所示.
(1)求这个抛物线的解析式;
(2)设(1)中的抛物线与![]() 轴的另一个交点为
轴的另一个交点为![]() ,抛物线的顶点为
,抛物线的顶点为![]() ,试求出点
,试求出点![]() ,
,![]() 的坐标,并判断
的坐标,并判断![]() 的形状;
的形状;
(3)点![]() 是直线
是直线![]() 上的一个动点(点
上的一个动点(点![]() 不与点
不与点![]() 和点
和点![]() 重合),过点
重合),过点![]() 作
作![]() 轴的垂线,交抛物线于点
轴的垂线,交抛物线于点![]() ,点
,点![]() 在直线
在直线![]() 上,距离点
上,距离点![]() 为
为![]() 个单位长度,设点
个单位长度,设点![]() 的横坐标为
的横坐标为![]() ,
,![]() 的面积为
的面积为![]() ,求出
,求出![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在当前国际“新冠肺炎”疫情防控的紧要关头,“中国制造”呈现出强大实力.据国家海关总局统计,4月25日当天,中国的口罩出口量就达10.6亿只.将数10.6亿用科学记数法表示为m![]() 10n,那么m,n的值分别为()
10n,那么m,n的值分别为()
A.10.6,8B.10.6,9C.1.06,9D.1.06,10
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com