
【题目】(概念认识)
若以三角形某边上任意一点为圆心,所作的半圆上的所有点都在该三角形的内部或边上,则将符合条件且半径最大的半圆称为该边关联的极限内半圆.
如图①,点P是锐角△ABC的边BC上一点,以P为圆心的半圆上的所有点都在△ABC的内部或边上.当半径最大时,半圆P为边BC关联的极限内半圆.
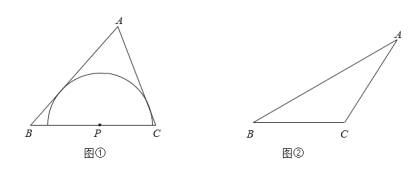
(初步思考)
(1)若等边△ABC的边长为1,则边BC关联的极限内半圆的半径长为 .
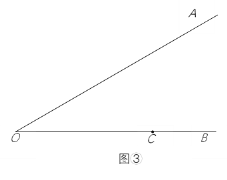
(2)如图②,在钝角△ABC中,用直尺和圆规作出边BC关联的极限内半圆(保留作图痕迹,不写作法).
(深入研究)
(3)如图③,∠AOB=30°,点C在射线OB上,OC=6,点Q是射线OA上一动点.在△QOC中,若边OC关联的极限内半圆的半径为r,当1≤r≤2时,求OQ的长的取值范围.
【答案】(1)![]() ;(2)见解析;(3)OQ≥
;(2)见解析;(3)OQ≥![]() -
-![]()
【解析】
(1)过P作AB垂线交于D点,根据直角三角形即可得出半径;
(2)过点C作BC的垂线交AB于点D,再作∠BDC的平分线交BC于点P.以点P为圆心,CP为半径在△ABC的内部作半圆即可.
(3)分情况讨论,当r=1时,OQ取得最小值,设QM=x,解直角三角形可求得OP=2,,OM=![]() ,解Rt△PCN,可得到CN=
,解Rt△PCN,可得到CN=![]() .OQ=OM+MQ=
.OQ=OM+MQ=![]() +x,CQ=CN+NQ=
+x,CQ=CN+NQ=![]() +x,根据S△OPQ∶S△CPQ=OP∶PC=1∶2,PM=PN,得出OQ∶QC=1∶2,所以QC=2OQ,则
+x,根据S△OPQ∶S△CPQ=OP∶PC=1∶2,PM=PN,得出OQ∶QC=1∶2,所以QC=2OQ,则![]() +x=2(
+x=2(![]() +x),x=
+x),x=![]() -2
-2![]() ,所以OQ=
,所以OQ=![]() -
-![]() .当r=2时,半圆P经过点C,过点C作OB的垂线交OA于点D.由(2)知,当Q在射线DA上时,OQ
.当r=2时,半圆P经过点C,过点C作OB的垂线交OA于点D.由(2)知,当Q在射线DA上时,OQ![]() 4
4![]() ,均符合题意.整合结果可得,当1≤r≤2时,OQ
,均符合题意.整合结果可得,当1≤r≤2时,OQ![]()
![]() -
-![]() .
.
解:(1)如图,过P作AB垂线交于D点,
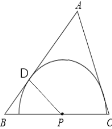
∵△ABC为等边三角形,边长为1,
∴∠DBP=60°,BP=![]() ,
,
∴R=DP=BP×sin60°=![]() .
.
(2)过点C作BC的垂线交AB于点D,再作∠BDC的平分线交BC于
点P.以点P为圆心,CP为半径在△ABC的内部作半圆,如图:
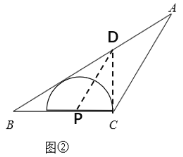
(3)当r=1时,OQ取得最小值.
如图①,半圆P与OQ、QC分别相切于点M、N,连接PQ.
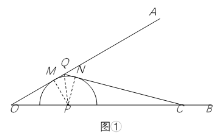
设QM=x,则QN=QM=x.
在Rt△OPM中,∠OMP=90°,∠AOB=30°,PM=1,
∵sin∠AOB=![]() ,tan∠AOB=
,tan∠AOB=![]() ,
,
∴OP=![]() =2,OM=
=2,OM=![]() =
=![]() .
.
∴PC=OC-OP=4.
在Rt△PCN中,∠PNC=90°,PN=1,PC=4,
∴CN=![]() =
=![]() .
.
∴OQ=OM+MQ=![]() +x,CQ=CN+NQ=
+x,CQ=CN+NQ=![]() +x.
+x.
∵S△OPQ∶S△CPQ=OP∶PC=1∶2,且PM=PN,
∴OQ∶QC=1∶2.
∴QC=2OQ.
∴![]() +x=2(
+x=2(![]() +x),
+x),
解得x=![]() -2
-2![]() .
.
∴OQ=![]() -2
-2![]() .
.
当r=2时,半圆P经过点C.
如图②,过点C作OB的垂线交OA于点D.
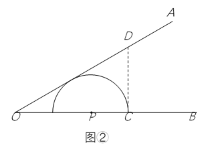
由(2)知,当Q在射线DA上时,OQ![]() 4
4![]() ,均符合题意.
,均符合题意.
∴当1![]() r
r![]() 2时,OQ
2时,OQ![]()
![]() -
-![]() .
.


科目:初中数学 来源: 题型:
【题目】已知:![]() 和
和![]() 都是等边三角形,点
都是等边三角形,点![]() 在边
在边![]() 上,连接
上,连接![]() .
.
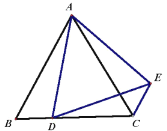
(1)如图1,求证:![]() ;
;
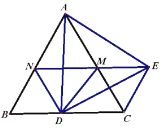
(2)如图2,点![]() 在
在![]() 上,
上,![]() (
(![]() ),连接
),连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() ,在不添加任何辅助线的情况下,请直接写出图2中所有与线段
,在不添加任何辅助线的情况下,请直接写出图2中所有与线段![]() 相等的线段(线段
相等的线段(线段![]() 除外).
除外).
查看答案和解析>>
科目:初中数学 来源: 题型:
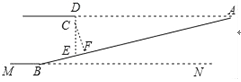
【题目】为缓解交通压力,市郊某地正在修建地铁站,拟同步修建地下停车库.如图是停车库坡道入口的设计图,其中MN是水平线,MN∥AD,AD⊥DE,CF⊥AB,垂足分别为D,F,坡道AB的坡度=1:3,AD=9米,点C在DE上,CD=0.5米,CD是限高标志牌的高度(标志牌上写有:限高 米).如果进入该车库车辆的高度不能超过线段CF的长,则该停车库限高多少米?(结果精确到0.1米,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈3.16)
≈3.16)
查看答案和解析>>
科目:初中数学 来源: 题型:
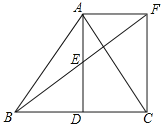
【题目】如图,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交BE的延长线于F,且AF=CD,连接CF.
(1)求证:△AEF≌△DEB;
(2)若AB=AC,试判断四边形ADCF的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】疫情期间的某一天,“建邺云课堂”为学生提供了语文、数学、英语三个学科各一节微课,甲、乙两名同学随机选择一节微课自主学习.
(1)甲同学选择数学微课的概率是 ;
(2)求甲、乙两名同学选择同一学科微课的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,且AB为⊙O的直径.∠ACB的平分线交⊙O于点D,过点D作⊙O的切线PD交CA的延长线于点P,过点A作AE⊥CD于点E,过点B作BF⊥CD于点F.
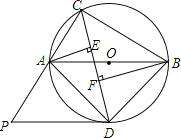
(1)求证:EF +AE= BF ;
(2)求证:△PDA∽△PCD ;
(3)若AC=6,BC=8,求线段PD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,⊙O与⊙P相交于A、B两点,点P在⊙O上,⊙O的弦AC切⊙P于点A,CP及其延长线交⊙P于D、E,经过E作EF⊥CE交CB的延长线于F.
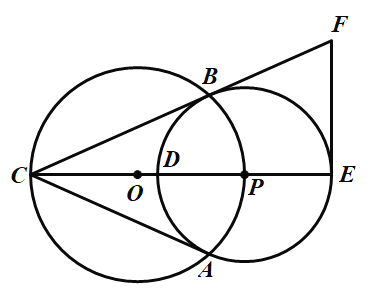
⑴求证:BC是⊙P的切线;
⑵若CD=2,CB=![]() ,求EF的长;
,求EF的长;
⑶若设k=PE:CE,是否存在实数k,使△PBD恰好是等边三角形?若存在,求出k的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
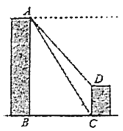
【题目】如图,甲、乙两座建筑物的水平距离![]() 为
为![]() ,从甲的顶部
,从甲的顶部![]() 处测得乙的顶部
处测得乙的顶部![]() 处的俯角为48°,测得底部
处的俯角为48°,测得底部![]() 处的俯角为58°,求乙建筑物
处的俯角为58°,求乙建筑物![]() 的高度.(参考数据:
的高度.(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() .结果取整数)
.结果取整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 的图像经过点
的图像经过点![]() ,
,![]() ,其对称轴为直线
,其对称轴为直线![]() :
:![]() ,过点
,过点![]() 作
作![]() 轴交抛物线于点
轴交抛物线于点![]() ,
,![]() 的平分线交线段
的平分线交线段![]() 于点
于点![]() ,点
,点![]() 是抛物线上的一个动点,设其横坐标为
是抛物线上的一个动点,设其横坐标为![]() .
.
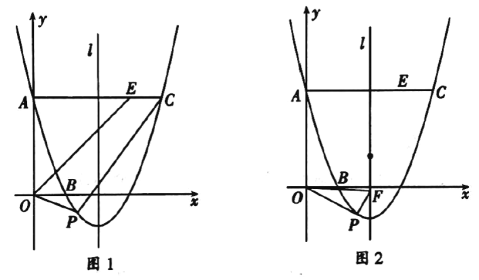
(1)求抛物线的解析式;
(2)如图1,动点![]() 在直线
在直线![]() 下方的抛物线上,连结
下方的抛物线上,连结![]() ,当
,当![]() 为何值时,四边形
为何值时,四边形![]() 面积最大,并求出其最大值,
面积最大,并求出其最大值,
(3)如图②,![]() 是抛物线的对称轴
是抛物线的对称轴![]() 上的一点,连接
上的一点,连接![]() ,在抛物线
,在抛物线![]() 轴下方的图像上是否存在点
轴下方的图像上是否存在点![]() 使
使![]() 满足:①
满足:①![]() ;②
;②![]() ?若存在,求点
?若存在,求点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com