
【题目】已知:如图,⊙O与⊙P相交于A、B两点,点P在⊙O上,⊙O的弦AC切⊙P于点A,CP及其延长线交⊙P于D、E,经过E作EF⊥CE交CB的延长线于F.
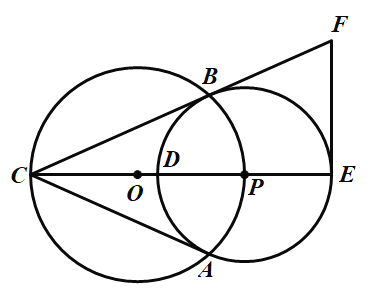
⑴求证:BC是⊙P的切线;
⑵若CD=2,CB=![]() ,求EF的长;
,求EF的长;
⑶若设k=PE:CE,是否存在实数k,使△PBD恰好是等边三角形?若存在,求出k的值;若不存在,请说明理由.
【答案】(1)见解析;(2)![]() ;(3)存在,
;(3)存在,![]()
【解析】
(1)要证明BC是⊙P的切线,则连接BP,需要证明BP⊥BC.根据已知条件,连接AP.根据切线的性质得到∠PAC=90°,再根据圆周角定理的推论得到CP是直径,从而得到∠CBP=90°,证明结论;
(2)首先证得△BCD∽△ECB,求得CE的长,再根据Rt△EFC∽Rt△BPC求得EF的长;
(3)根据等边三角形的性质和含30度角的直角三角形的性质进行求解.
(1)连接PA、PB,
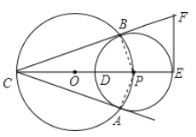
∵AC切⊙P于A,PA是⊙P的半径,
∴AC⊥PA.
即:∠PAC=90°,
∴CP是⊙O的直径,
∴∠PBC=90°,
即PB⊥CB,
又∵PB是⊙P的半径,
∴BC是⊙P的切线;
(2)连接BD、BE、PB,
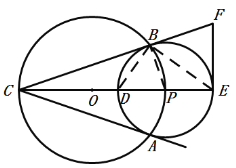
∵BC是⊙P的切线,
∴∠CBD=∠CEB,
又∠BCD=∠ECB,
∴△BCD∽△ECB,
∴![]() ,
,
∵CD=2,CB=![]() ,
,
∴CE= ,
,
DE=CE-CD=4-2=2.
∴PB=![]() DE =1,
DE =1,
在Rt△EFC和Rt△BPC中,∠ECF=∠BCP,∠FEC=∠PBC=90°,
∴Rt△EFC∽Rt△BPC,
∴![]() ,
,
∴![]() ;
;
(3)存在实数![]() 时,△PBD为等边三角形.
时,△PBD为等边三角形.
理由如下:
∵△PBD为等边三角形,
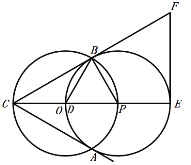
∴∠CPB=60°.
∵CB是⊙P的切线,
∴CB⊥BP,
∴∠BCP=30°,△PBC为直角三角形,
∴PB=![]() PC,PB=PE,
PC,PB=PE,
∴PC=2PE,CE=PC+PE,
∴CE=3PE,
∴PE:CE=1:3,
即:![]() 时,△PBD为等边三角形.
时,△PBD为等边三角形.
【点晴】
本题考查了切线的判定和切线的性质以及相似三角形的判定和相似三角形的性质,勾股定理的应用,含30度角的直角三角形的性质.


科目:初中数学 来源: 题型:
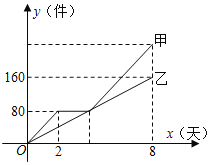
【题目】甲乙两个工厂同时加工一批机器零件.甲工厂先加工了两天后停止加工,维修设备,当维修完设备时,甲乙两厂加工的零件数相等,甲工厂再以原来的工作效率继续加工这批零件.甲乙两厂加工零件的数量y甲(件),y乙(件)与加工件的时间x(天)的函数图象如图所示,
(1)乙工厂每天加工零件的数为 件;
(2)甲工厂维修设备的时间是多少天?
(3)求甲维修设备后加工零件的数量y甲(件)与加工零件的时间x(天)的函数关系式,并写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
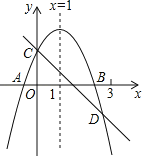
【题目】如图所示,已知二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C对称轴为直线x=1.直线y=﹣x+c与抛物线y=ax2+bx+c交于C、D两点,D点在x轴下方且横坐标小于3,则下列结论:
①2a+b+c>0;②a﹣b+c<0;③x(ax+b)≤a+b;④a<﹣1.
其中正确的有( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(概念认识)
若以三角形某边上任意一点为圆心,所作的半圆上的所有点都在该三角形的内部或边上,则将符合条件且半径最大的半圆称为该边关联的极限内半圆.
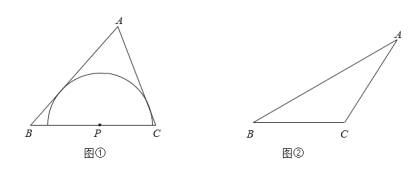
如图①,点P是锐角△ABC的边BC上一点,以P为圆心的半圆上的所有点都在△ABC的内部或边上.当半径最大时,半圆P为边BC关联的极限内半圆.
(初步思考)
(1)若等边△ABC的边长为1,则边BC关联的极限内半圆的半径长为 .
(2)如图②,在钝角△ABC中,用直尺和圆规作出边BC关联的极限内半圆(保留作图痕迹,不写作法).
(深入研究)
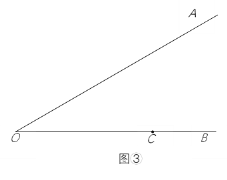
(3)如图③,∠AOB=30°,点C在射线OB上,OC=6,点Q是射线OA上一动点.在△QOC中,若边OC关联的极限内半圆的半径为r,当1≤r≤2时,求OQ的长的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解初三学生的体育锻炼时间,小华调查了某班45名同学一周参加体育锻炼的情况,并把它绘制成折线统计图(如图所示).那么关于该班45名同学一周参加体育锻炼时间的说法错误的是( )
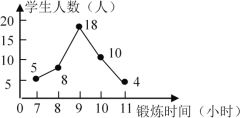
A.众数是9
B.中位数是9
C.平均数是9
D.锻炼时间不低于9小时的有14人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C为⊙O上一点,AE和过点C的切线互相垂直,垂足为E,AE交⊙O于点D,直线EC交AB的延长线于点P,连接AC,BC,PB:PC=1:2.

(1)求证:AC平分∠BAD;
(2)探究线段PB,AB之间的数量关系,并说明理由;
(3)若AD=3,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=x2﹣2x+k与x轴交于A、B两点,与y轴交于点C(0,﹣3).[图2、图3为解答备用图]
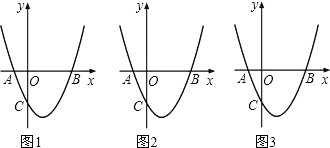
(1)k= ,点A的坐标为 ,点B的坐标为 ;
(2)设抛物线y=x2﹣2x+k的顶点为M,求四边形ABMC的面积;
(3)在x轴下方的抛物线上是否存在一点D,使四边形ABDC的面积最大?若存在,请求出点D的坐标;若不存在,请说明理由;
(4)在抛物线y=x2﹣2x+k上求点Q,使△BCQ是以BC为直角边的直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“六一”儿童节前,玩具商店根据市场调查,用2500元购进一批儿童玩具,上市后很快脱销,接着又用4500元购进第二批这种玩具,所购数量是第一批数量的1.5倍,但每套进价多了10元.第一、二批玩具每套的进价分别是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com