
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于点
的图象交于点![]() ,
,![]() ,点
,点![]() 在以
在以![]() 为圆心,
为圆心,![]() 为半径的⊙
为半径的⊙![]() 上,
上,![]() 是
是![]() 的中点,若
的中点,若![]() 长的最大值为
长的最大值为![]() ,则
,则![]() 的值为__________.
的值为__________.
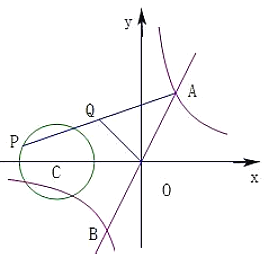
【答案】![]()
【解析】
由三角形中位线的性质可知BP长的最大值为3,此时BP过圆心C,过B作BD⊥x轴于D,设B(t,2t),则CD= t+2,BD=2t,在Rt△BCD中,根据勾股定理即可求得t的值,再根据反比例函数图像上点的坐标特征即可求出k的值.
连接BP,
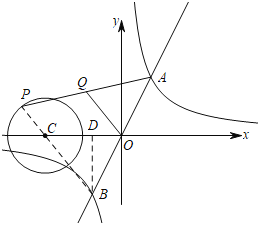
由对称性得:OA=OB,
∵Q是AP的中点,
∴OQ=12BP,
∵OQ长的最大值为![]() ,
,
∴BP长的最大值为![]() ×2=3,
×2=3,
如图,当BP过圆心C时,BP最长,过B作BD⊥x轴于D,
∵CP=1,
∴BC=2,
∵B在直线y=2x上,
设B(t,2t),则CD=t(2)=t+2,BD=2t,
在Rt△BCD中,由勾股定理得:;BC2=CD2+BD2,
∴22=(t+2)2+(2t)2,
t=0(舍)或![]() ,
,
∴B(![]() ,
,![]() ),
),
∵点B在反比例函数y=![]() (k>0)的图象上,
(k>0)的图象上,
∴k=![]() ×(
×(![]() )=
)=![]() ;
;
故答案为![]() .
.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:
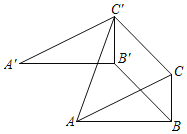
【题目】定义:有一组邻边相等的凸四边形叫做等邻边四边形.如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=1,将△ABC沿∠ABC的平分线BB'的方向平移,得到A'B'C',连接AC',CC',若四边形ABCC'是等邻边四边形,则平移距离BB'的长度是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A(2,y1),B(﹣3,y2),C(﹣5,y3)三个点都在反比例函数![]() 的图象上,比较y1,y2,y3的大小,则下列各式正确的是( )
的图象上,比较y1,y2,y3的大小,则下列各式正确的是( )
A.y1<y2<y3B.y2<y3<y1C.y1<y3<y2D.y3<y2<y1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小魏探究学习函数的经验,对函数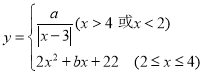 的图像与性质进行了研究,下面是小魏的探究过程,请补充完整.
的图像与性质进行了研究,下面是小魏的探究过程,请补充完整.
(1)下表是![]() 与
与![]() 的几组对应值:
的几组对应值:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
请直接写出:![]() _______,
_______,![]() ______,
______,![]() _______.
_______.
(2)画出该函数图像.
(3)写出该函数的一条性质:_______________.
(4)一次函数![]() 与该函数图像至少有三个交点,则
与该函数图像至少有三个交点,则![]() 的范围_______.
的范围_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】横、纵坐标均为整数的点称为格点,如图,![]() 的三个顶点
的三个顶点![]() ,
,![]() ,
,![]() 均为格点,
均为格点,![]() 上的点
上的点![]() 也为格点,用无刻度的直尺作图:
也为格点,用无刻度的直尺作图:
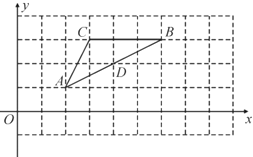
(1)将线段![]() 绕点
绕点![]() 顺时针旋转90°,得到线段
顺时针旋转90°,得到线段![]() ,写出格点
,写出格点![]() 的坐标;
的坐标;
(2)将线段![]() 平移至线段
平移至线段![]() ,使点
,使点![]() 与点
与点![]() 重合,直接写出格点
重合,直接写出格点![]() 的坐标;
的坐标;
(3)画出线段![]() 关于
关于![]() 对称的线段
对称的线段![]() ,保留作图痕迹.
,保留作图痕迹.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像交于点
的图像交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,且
,且![]() .
.

(1)求反比例函数与一次函数的表达式;
(2)若点![]() 为
为![]() 轴上一点,
轴上一点,![]() 是等腰三角形,求点
是等腰三角形,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
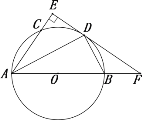
【题目】如图,AB是⊙O的直径,AD平分∠BAC交⊙O于D,过D作DE⊥AC交AC延长线于点E,交AB延长线于点F.
(1)求证:EF是⊙O的切线;
(2)若DE=![]() ,tan∠BDF=
,tan∠BDF=![]() ,求DF的长.
,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市计划购进甲、乙两种商品,两种商品的进价、售价如下表:
商品 | 甲 | 乙 |
进价(元/件) |
|
|
售价(元/件) | 200 | 100 |
若用360元购进甲种商品的件数与用180元购进乙种商品的件数相同.
(1)求甲、乙两种商品的进价是多少元?
(2)若超市销售甲、乙两种商品共50件,其中销售甲种商品为![]() 件(
件(![]() ),设销售完50件甲、乙两种商品的总利润为
),设销售完50件甲、乙两种商品的总利润为![]() 元,求
元,求![]() 与
与![]() 之间的函数关系式,并求出
之间的函数关系式,并求出![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗,我市某食品厂为了解市民对去年销量较好的肉馅粽(咸)、豆沙馅粽(甜)、红枣馅粽(甜)、蛋黄馅粽(咸)(以下分别用A、B、C、D表示)这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).
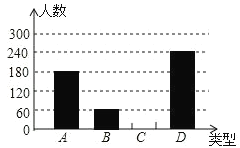
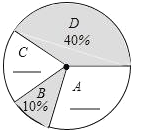
请根据以上信息回答:
(1)本次参加抽样调查的市民有多少人?
(2)将两幅不完整的图补充完整;
(3)若有外型完全相同的A、B、C、D粽各一个,煮熟后,小王吃了两个,用列表或画树状图的方法,求他吃到的两个粽子都是甜味的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com