
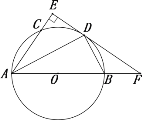
【题目】如图,AB是⊙O的直径,AD平分∠BAC交⊙O于D,过D作DE⊥AC交AC延长线于点E,交AB延长线于点F.
(1)求证:EF是⊙O的切线;
(2)若DE=![]() ,tan∠BDF=
,tan∠BDF=![]() ,求DF的长.
,求DF的长.
【答案】(1)证明见解析;(2)DF=4.
【解析】
(1)连接OD,证明OD∥AE,∠ODF=90°,问题得证;
(2)证明∠BDF=∠DAE=∠BAD,依次求出AE、AD、DB、AB,证明△FBD∽△FDA,相似比为1:2,![]() ,求出BF,DF.
,求出BF,DF.
(1)连接OD
∵AD平分∠FAC,
∴∠BAD=∠DAE
∵OA=OD,∴∠OAD=∠ODA,
∴∠DAE=∠ODA,
∴OD∥AE,∴∠E=∠ODF
∵DE⊥AC,
∴∠E=90°,
∴∠ODF=90°,
∴OD⊥EF,∴EF是⊙O的切线.
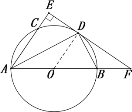
(2)∵AB为直径,∴∠ADB=90°,
∴∠ADE+∠BDF=90°,
∵∠E=90°,∴∠ADE+∠DAE=90°
∴∠BDF=∠DAE,∵∠BAD=∠DAE
∴∠BDF=∠DAE=∠BAD
∵tan∠BDF=![]() ,
,
∴tan∠BDF=tan∠DAE=tan∠BAD=![]()
∴![]() ,
,
∵DE=![]() ,∴AE=
,∴AE=![]() ,AD=
,AD=![]()
∴BD=![]() ,∴AB=6
,∴AB=6
又∠F=∠F,∠BDF=∠BAD
∴△FBD∽△FDA,
∴![]() ,∴DF=2BF,
,∴DF=2BF,![]()
∴![]() ,又BA=6
,又BA=6
∴BF=2,∴DF=4


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:初中数学 来源: 题型:
【题目】图1是一辆吊车的实物图,图2是其工作示意图,![]() 是可以伸缩的起重臂,其转动点
是可以伸缩的起重臂,其转动点![]() 离地面
离地面![]() 的高度
的高度![]() 为
为![]() .当起重臂
.当起重臂![]() 长度为
长度为![]() ,张角
,张角![]() 为118°.
为118°.
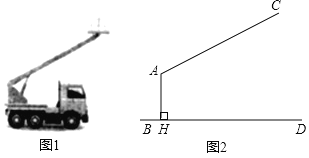
(1)求操作平台![]() 离地面的高度;
离地面的高度;
(2)当张角![]() 为120°,其它条件不变时,求操作平台
为120°,其它条件不变时,求操作平台![]() 升高的高度.
升高的高度.
(最后结果精确到0.1,参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
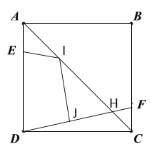
【题目】如图,正方形![]() 边长为
边长为![]() ,
,![]() ,
,![]() 分别为线段
分别为线段![]() ,
,![]() 上一点,且
上一点,且![]() ,
,![]() ,
,![]() 与
与![]() 相交于
相交于![]() ,
,![]() 为线段
为线段![]() 上一点(不与端点重合),
上一点(不与端点重合),![]() 为线段
为线段![]() 上一点(不与端点重合),则
上一点(不与端点重合),则![]() 的最小值为( )
的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
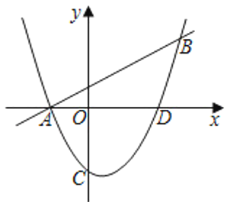
【题目】如图,一次函数y=![]() x+1的图象与二次函数y=
x+1的图象与二次函数y=![]() x2+bx+c的图象交于A,B两点,点A在x轴上.点B的横坐标为4.
x2+bx+c的图象交于A,B两点,点A在x轴上.点B的横坐标为4.
(1)b= ,c= ;
(2)设二次函数的图象与y轴交于C点,与x轴的另一个交点为D.连接AC,CD,求∠ACD的正弦值;
(3)若M点在x轴下方二次函数图象上,
①过M点作y轴平行线交直线AB于点E,以M点为圆心,ME的长为半径画圆,求圆M在直线AB上截得的弦长的最大值;
②若∠ABM=∠ACO,则点M的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着《流浪地球》的热播,其同名科幻小说的销量也急剧上升.为应对这种变化,某网店分别花20000元和30000元先后两次增购该小说,第二次的数量比第一次多500套,且两次进价相同.
(1)该科幻小说第一次购进多少套?
(2)根据以往经验:当销售单价是25元时,每天的销售量是250套;销售单价每上涨1元,每天的销售量就减少10套.网店要求每套书的利润不低于10元且不高于18元.
①直接写出网店销售该科幻小说每天的销售量y(套)与销售单价x(元)之间的函数关系式及自变量x的取值范围;
②网店决定每销售1套该科幻小说,就捐赠a(0<a<7)元给困难职工,每天扣除捐赠后可获得的最大利润为1960元,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
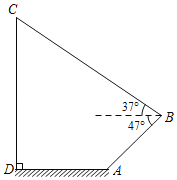
【题目】如图,一架无人机在距离地面高度为21.4米的点B处,测得地面点A的俯角为47°,接着,这架无人机从点B沿仰角为37°的方向继续飞行20![]() 米到达点C,此时测得点C恰好在地面点D的正上方,且A,D两点在同一水平线上,求A,D两点之间的距离.(结果精确到1米;参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,sin47°≈0.73,cos47°≈0.68,tan47°≈1.07,
米到达点C,此时测得点C恰好在地面点D的正上方,且A,D两点在同一水平线上,求A,D两点之间的距离.(结果精确到1米;参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,sin47°≈0.73,cos47°≈0.68,tan47°≈1.07,![]() ≈2.45)
≈2.45)
查看答案和解析>>
科目:初中数学 来源: 题型:
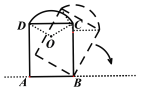
【题目】如图,竖直放置的一个铝合金窗框由矩形和弧形两部分组成,AB=![]() m,AD= 2m,弧CD所对的圆心角为∠COD=120°.现将窗框绕点B顺时针旋转横放在水平的地面上,这一过程中,窗框上的点到地面的最大高度为__m.
m,AD= 2m,弧CD所对的圆心角为∠COD=120°.现将窗框绕点B顺时针旋转横放在水平的地面上,这一过程中,窗框上的点到地面的最大高度为__m.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com