
【题目】如图,△ABC内接于⊙O,且AB为⊙O的直径.∠ACB的平分线交⊙O于点D,过点D作⊙O的切线PD交CA的延长线于点P,过点A作AE⊥CD于点E,过点B作BF⊥CD于点F.
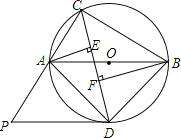
(1)求证:EF +AE= BF ;
(2)求证:△PDA∽△PCD ;
(3)若AC=6,BC=8,求线段PD的长.
【答案】(1)详见解析;(2)详见解析;(3)![]()
【解析】
(1)利用圆的性质,证明△ADE≌△DBF可得到结论,
(2)连接OD,证明∠PDA=∠ACD=∠ADO =45°,从而可得结论,
(3)利用圆的性质,得到△ACE,△DAB为等腰直角三角形,求解![]() 的长,利用△PDA∽△PCD,从而可得答案.
的长,利用△PDA∽△PCD,从而可得答案.
(1)证明:![]() 为直径,
为直径,
![]()
∵∠ACB的平分线交⊙O于点D,
∴∠ACD=∠BCD=45°,
∴![]()
∴AD=BD
∵AB是⊙O的直径,
∴∠ADB=∠ADE+∠BDF=90°,
∵AE⊥CD,BF⊥CD,
∴∠AED=∠BFD=90°,
∴∠FBD+∠BDF=90°,
∴∠FBD=∠ADE,
在△ADE和△DBF中
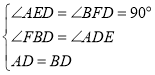 ,
,
∴△ADE≌△DBF(AAS)
∴BF=DE,AE=DF,
∵EF + DF = DE
∴EF + AE = BF

(2)证明:如图,连接OD
∵∠ACD=∠BCD=45°,
∴AD=BD
∴∠DAB=∠ABD=45°.
∴△DAB为等腰直角三角形.
∵AB是直径,O是圆心
∴∠ACD=∠ADO=∠BDO =45°.
∵PD为⊙O的切线,
∴OD⊥PD.
∴∠PDA=∠ACD=∠ADO =45°.
又∵∠DPA=∠CPD,
∴△PDA∽△PCD,
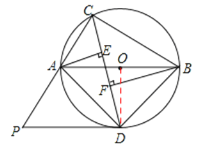
(3)在Rt△ACB中,![]()
∵△DAB为等腰直角三角形,
∴AD=DB=![]() ,
,
∵AE⊥CD,∠ACD=45°
∴△ACE为等腰直角三角形.
∴AE=CE=![]()
在Rt△AED中,
![]()
![]()
∵△PDA∽△PCD.
∴![]() .
.
∴PA=![]() ,PC=
,PC=![]() .
.
又PC=PA+AC,
∴![]() +6=
+6=![]() ,
,
解得:PD=![]()


科目:初中数学 来源: 题型:
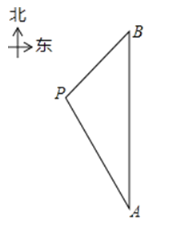
【题目】在一次海上救援中,两艘专业救助船![]() 同时收到某事故渔船的求救讯息,已知此时救助船
同时收到某事故渔船的求救讯息,已知此时救助船![]() 在
在![]() 的正北方向,事故渔船
的正北方向,事故渔船![]() 在救助船
在救助船![]() 的北偏西30°方向上,在救助船
的北偏西30°方向上,在救助船![]() 的西南方向上,且事故渔船
的西南方向上,且事故渔船![]() 与救助船
与救助船![]() 相距120海里.
相距120海里.
(1)求收到求救讯息时事故渔船![]() 与救助船
与救助船![]() 之间的距离;
之间的距离;
(2)若救助船A,![]() 分别以40海里/小时、30海里/小时的速度同时出发,匀速直线前往事故渔船
分别以40海里/小时、30海里/小时的速度同时出发,匀速直线前往事故渔船![]() 处搜救,试通过计算判断哪艘船先到达.
处搜救,试通过计算判断哪艘船先到达.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=2,AD=4,点E在边BC上,把△DEC沿DE翻折后,点C落在C′处.若△ABC′恰为等腰三角形,则CE的长为__________.
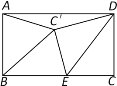
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(概念认识)
若以三角形某边上任意一点为圆心,所作的半圆上的所有点都在该三角形的内部或边上,则将符合条件且半径最大的半圆称为该边关联的极限内半圆.
如图①,点P是锐角△ABC的边BC上一点,以P为圆心的半圆上的所有点都在△ABC的内部或边上.当半径最大时,半圆P为边BC关联的极限内半圆.
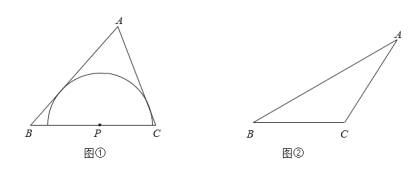
(初步思考)
(1)若等边△ABC的边长为1,则边BC关联的极限内半圆的半径长为 .
(2)如图②,在钝角△ABC中,用直尺和圆规作出边BC关联的极限内半圆(保留作图痕迹,不写作法).
(深入研究)
(3)如图③,∠AOB=30°,点C在射线OB上,OC=6,点Q是射线OA上一动点.在△QOC中,若边OC关联的极限内半圆的半径为r,当1≤r≤2时,求OQ的长的取值范围.
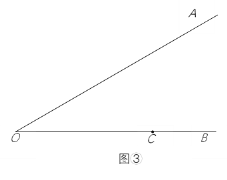
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象分别交x轴、y轴于A、B两点,与反比例函数![]() 的图象交于C、D两点,DE⊥x轴于点E,已知C点的坐标是(6,-1),DE=3.
的图象交于C、D两点,DE⊥x轴于点E,已知C点的坐标是(6,-1),DE=3.
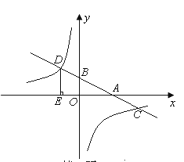
(1)求反比例函数与一次函数的解析式.
(2)根据图象写出不等式kx+b>![]() 的解集.
的解集.
(3)连接OC、OD,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋中装有2个黄球,1个红球和1个白球,除色外都相同.
(1)搅匀后,从袋中随机出一个球,恰好是黄球的概是_____?
(2)搅匀后,从中随机摸出两个球,求摸到一个红球和一个黄球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读理解)
我们将使得函数值为零的自变量的值称为函数的零点值,此时的点称为函数的零点.例如,对于函数y=x-1,令y=0,可得x=1,我们就说1是函数y=x-1的零点值,点(1,0)是函数y=x-1的零点.
(问题解决)
(1)已知函数![]() ,则它的零点坐标为________;
,则它的零点坐标为________;
(2)若二次函数y=x2-2x+m有两个零点,则实数m的取值范围是________;
(3)已知二次函数![]() 的两个零点都是整数点,求整数k的值.
的两个零点都是整数点,求整数k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com