
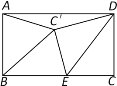
【题目】如图,在矩形ABCD中,AB=2,AD=4,点E在边BC上,把△DEC沿DE翻折后,点C落在C′处.若△ABC′恰为等腰三角形,则CE的长为__________.
科目:初中数学 来源: 题型:
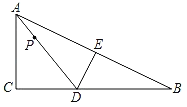
【题目】如图,在△ABC中,∠C=90°,AC=8,BC=16,点D在边BC上,沿DE将△ABC折叠,使点B与点A重合,连接AD,点P在线段AD上,当点P到△ABC的直角边距离等于5时,AP的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
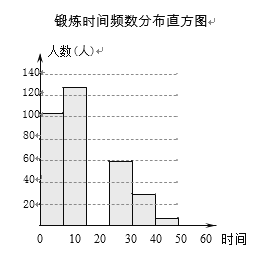
【题目】某数学活动小组为了解全县九年级学生在抗新冠病毒疫情期间平均每天居家锻炼时间,向全县部分学生进行了抽样调查,并将收集到的数据整理成如图的统计图(部分数据未标出).
(1)这次抽样调查的学生人数一共有 人;
(2)求频数分布表中 a 的值,并补全频数分布直方图; ,
(3)若该县有 5000 名九年级学生,请你估计全县九年级学生平均每天居家锻炼时间不超过20分钟的有多少人?
时间 x/分 | 人数/人 | 频率 |
0<x≤10 | 102 | 25.5% |
10<x≤20 | 132 | 33% |
20<x≤30 | a | 17.5% |
30<x≤40 | 59 | 14.75% |
40<x≤50 | 29 | 7.25% |
50<x≤60 | 8 | 2% |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于A、B两点,与
轴交于A、B两点,与![]() 轴交于点C,四边形OBHC为矩形,CH的延长线交抛物线于点D(5,-2),连接BC、AD.
轴交于点C,四边形OBHC为矩形,CH的延长线交抛物线于点D(5,-2),连接BC、AD.
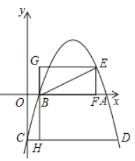
(1)将矩形OBHC绕点B按逆时针旋转90°后,再沿![]() 轴对折到矩形GBFE(点C与点E对应,点O与点G对应),求点E的坐标;
轴对折到矩形GBFE(点C与点E对应,点O与点G对应),求点E的坐标;
(2)设过点E的直线交AB于点P,交CD于点Q.
①当四边形PQCB为平行四边形时,求点P的坐标;
②是否存在点P,使直线PQ分梯形ADCB的面积为1∶3两部分?若存在,求出点P坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
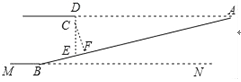
【题目】为缓解交通压力,市郊某地正在修建地铁站,拟同步修建地下停车库.如图是停车库坡道入口的设计图,其中MN是水平线,MN∥AD,AD⊥DE,CF⊥AB,垂足分别为D,F,坡道AB的坡度=1:3,AD=9米,点C在DE上,CD=0.5米,CD是限高标志牌的高度(标志牌上写有:限高 米).如果进入该车库车辆的高度不能超过线段CF的长,则该停车库限高多少米?(结果精确到0.1米,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈3.16)
≈3.16)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在矩形ABCD中,AD=10cm,AB=4cm,动点P从点A出发,以2cm/s的速度沿AD向终点D移动,设移动时间为![]() (s) .连接PC,以PC为一边作正方形PCEF,连接DE、DF.
(s) .连接PC,以PC为一边作正方形PCEF,连接DE、DF.
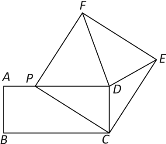
(1)求正方形PCEF的面积(用含![]() 的代数式来表示,不要求化简),并求当正方形PCEF的面积为25 cm2时
的代数式来表示,不要求化简),并求当正方形PCEF的面积为25 cm2时![]() 的值;
的值;
(2)设△DEF的面积为![]() (cm2),求
(cm2),求![]() 与
与![]() 之间的函数关系式,并求当
之间的函数关系式,并求当![]() 为何值时?△DEF的面积取得最小值,这个最小值是多少?
为何值时?△DEF的面积取得最小值,这个最小值是多少?
(3)求当![]() 为何值时?△DEF为等腰三角形.
为何值时?△DEF为等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
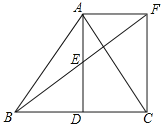
【题目】如图,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交BE的延长线于F,且AF=CD,连接CF.
(1)求证:△AEF≌△DEB;
(2)若AB=AC,试判断四边形ADCF的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,且AB为⊙O的直径.∠ACB的平分线交⊙O于点D,过点D作⊙O的切线PD交CA的延长线于点P,过点A作AE⊥CD于点E,过点B作BF⊥CD于点F.
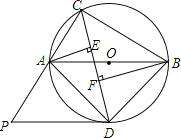
(1)求证:EF +AE= BF ;
(2)求证:△PDA∽△PCD ;
(3)若AC=6,BC=8,求线段PD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
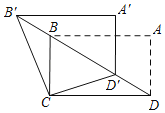
【题目】如图,在矩形ABCD中,AB=![]() ,BC=1,将△ABD沿射线DB平移得到△A'B'D',连接B′C,D′C,则B'C+D'C的最小值是_____.
,BC=1,将△ABD沿射线DB平移得到△A'B'D',连接B′C,D′C,则B'C+D'C的最小值是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com