
【题目】如图,抛物线![]() 与
与![]() 轴交于A、B两点,与
轴交于A、B两点,与![]() 轴交于点C,四边形OBHC为矩形,CH的延长线交抛物线于点D(5,-2),连接BC、AD.
轴交于点C,四边形OBHC为矩形,CH的延长线交抛物线于点D(5,-2),连接BC、AD.
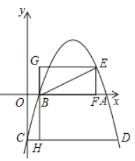
(1)将矩形OBHC绕点B按逆时针旋转90°后,再沿![]() 轴对折到矩形GBFE(点C与点E对应,点O与点G对应),求点E的坐标;
轴对折到矩形GBFE(点C与点E对应,点O与点G对应),求点E的坐标;
(2)设过点E的直线交AB于点P,交CD于点Q.
①当四边形PQCB为平行四边形时,求点P的坐标;
②是否存在点P,使直线PQ分梯形ADCB的面积为1∶3两部分?若存在,求出点P坐标;若不存在,请说明理由.
【答案】(1)E(3,1);(2)①P(![]() ,0);②存在,(
,0);②存在,(![]() ,0)或(
,0)或(![]() ,0)
,0)
【解析】
(1)由于旋转翻折只是图形的位置有变化,而大小不变,因此:△BCH≌△BEF,OC=BF,
CH=EF,OC的长可以通过C点的坐标得出,求CH即OB的长,要先得出B点的坐标,可通过抛物线的解析式来求得,这样可得出E点的坐标,然后代入抛物线的解析式即可判断出E是否在抛物线上;
(2)①设P(m,0),根据四边形PQCB为平行四边形,BP∥CQ,得到BC//PQ,故可得出△EFP∽△BHC,所以![]() ,从而得
,从而得![]() ,解得m的值后即可求得点P的坐;
,解得m的值后即可求得点P的坐;
②可先设出P点的坐标如:(n,0),由于直线PQ过E点,因此可根据P,E的坐标用待定系数法表示出直线PQ的解析式,进而可求出Q点的坐标,这样就能表示出BP,AP,CQ,DQ的长,也就能表示出梯形BPQC和梯形APQD的面积,然后分类进行讨论:梯形BPQC的面积:梯形APQD的面积=1:3,梯形APQD的面积:梯形BPQC的面积=1:3,根据上述两种不同的比例关系式,可求出各自的n的取值,也就能求出不同的P点的坐标,综上所述可求出符合条件的P点的坐标.
解:(1)令y=0,得![]() ,
,
解得x1=1,x2=4,
∴A(4,0),B(1,0),
∴OA=4,OB=1,
由矩形的性质知:CH=OB=1,BH=OC=2,∠BHC=90°,
由旋转、对折性质可知:EF=1,BF=2,∠EFB=90°,
∴E(3,1);
(2)①设P(m,0),
∵四边形PQCB为平行四边形,BP∥CQ,
∴BC∥PQ,
∴![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴P(![]() ,0);
,0);
②存在;
设点P(n,0),延长EF交CD于点R,
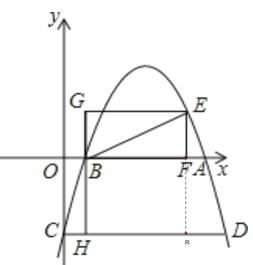
易得OF=CR=3,PB=n-1.
∵S梯形BCRF=5,S梯形ADRF=3,记S梯形BCQP=S1,S梯形ADQP=S2,
下面分两种情况:
第一种情况,当S1:S2=1:3时,![]() <5,
<5,
∴此时点P在点F(3,0)的左侧,则PF=3-n,
由△EPF∽△EQR,得![]() ,
,
则QR=9-3n,
∴CQ=3n-6,由S1=2,得![]() ,
,
解得![]() ;
;
∴点P的坐标为(![]() ,0),
,0),
第二种情况,当S1:S2=3:1时,![]() >5,
>5,
∴此时点P在点F(3,0)的右侧,则PF=n-3,
由△EPF∽△EQR,得QR=3n-9,
∴CQ=3n-6,由S1=6,得![]() ,
,
解得![]() ,
,
∴点P的坐标为(![]() ,0)
,0)
综上所述,所求点P的坐标为(![]() ,0)或(
,0)或(![]() ,0).
,0).


科目:初中数学 来源: 题型:
【题目】如图1,水平放置一个三角板和一个量角器,三角板的边AB和量角器的直径DE在一条直线上,∠ACB=90°,∠BAC=30°,OD=3cm,开始的时候BD=1cm,现在三角板以2cm/s的速度向右移动.
(1)当点B于点O重合的时候,求三角板运动的时间;
(2)三角板继续向右运动,当B点和E点重合时,AC与半圆相切于点F,连接EF,如图2所示.
①求证:EF平分∠AEC;
②求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
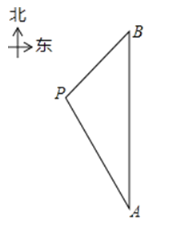
【题目】在一次海上救援中,两艘专业救助船![]() 同时收到某事故渔船的求救讯息,已知此时救助船
同时收到某事故渔船的求救讯息,已知此时救助船![]() 在
在![]() 的正北方向,事故渔船
的正北方向,事故渔船![]() 在救助船
在救助船![]() 的北偏西30°方向上,在救助船
的北偏西30°方向上,在救助船![]() 的西南方向上,且事故渔船
的西南方向上,且事故渔船![]() 与救助船
与救助船![]() 相距120海里.
相距120海里.
(1)求收到求救讯息时事故渔船![]() 与救助船
与救助船![]() 之间的距离;
之间的距离;
(2)若救助船A,![]() 分别以40海里/小时、30海里/小时的速度同时出发,匀速直线前往事故渔船
分别以40海里/小时、30海里/小时的速度同时出发,匀速直线前往事故渔船![]() 处搜救,试通过计算判断哪艘船先到达.
处搜救,试通过计算判断哪艘船先到达.
查看答案和解析>>
科目:初中数学 来源: 题型:
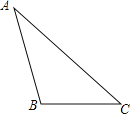
【题目】如图,已知钝角△ABC
(1)过点A作BC边的垂线,交CB的延长线于点D;(尺规作图,保留作图痕迹,不要求写作法)
(2)在(1)的条件下,若∠ABC=122°,BC=5,AD=4,求CD的长.(结果保留到0.1,参考数据:sin32°=0.53,cos32°=0.85,tan32°=0.62.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E,F分别为BC,CD的中点,连接AE,BF交于点G,将△BCF沿BF对折,得到△BPF,延长FP交BA延长于点Q,下列结论正确的有( )个.
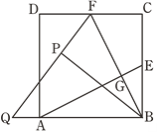
①AE⊥BF;②QB=QF;③![]() ;④SECPG=3S△BGE
;④SECPG=3S△BGE
A.1B.4C.3D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
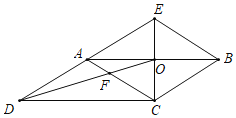
【题目】如图,CE是ABCD的边AB的垂直平分线,垂足为点O,CE与DA的延长线交于点E.连接AC,BE,DO,DO与AC交于点F,则下列结论:①四边形ACBE是菱形;②∠ACD=∠BAE;③AF:BE=2:3;④S四边形AFOE:S△COD=2:3;以上四个结论中所有正确的结论是( )
A.①②B.①②③C.②④D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
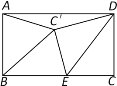
【题目】如图,在矩形ABCD中,AB=2,AD=4,点E在边BC上,把△DEC沿DE翻折后,点C落在C′处.若△ABC′恰为等腰三角形,则CE的长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋中装有2个黄球,1个红球和1个白球,除色外都相同.
(1)搅匀后,从袋中随机出一个球,恰好是黄球的概是_____?
(2)搅匀后,从中随机摸出两个球,求摸到一个红球和一个黄球的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com