【题目】在当前国际“新冠肺炎”疫情防控的紧要关头，“中国制造”呈现出强大实力．据国家海关总局统计，4月25日当天，中国的口罩出口量就达10.6亿只．将数10.6亿用科学记数法表示为m
10n，那么m，n的值分别为（）
A.10.6，8B.10.6，9C.1.06，9D.1.06，10
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
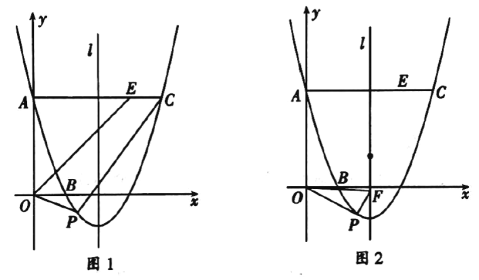
【题目】如图，已知抛物线
的图像经过点
，
，其对称轴为直线
：
，过点
作
轴交抛物线于点
，
的平分线交线段
于点
，点
是抛物线上的一个动点，设其横坐标为
．
(1)求抛物线的解析式;
(2)如图1，动点在直线
下方的抛物线上，连结
，当为何值时，四边形
面积最大，并求出其最大值，
(3)如图②，
是抛物线的对称轴上的一点，连接
，在抛物线
轴下方的图像上是否存在点使
满足:①
；②
？若存在，求点的坐标，若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB＝AC，以AB为直径的⊙O分别交AC，BC于点D，E，点F在AC的延长线上，且∠BAC＝2∠CBF．
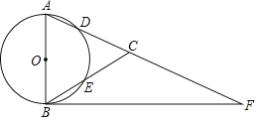
（1）求证：BF是⊙O的切线；
（2）若⊙O的直径为3，sin∠CBF＝
，求BC长．
查看答案和解析>>
科目：初中数学 来源： 题型：
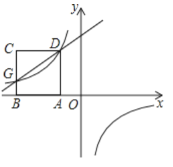
【题目】如图，正方形ABCD的顶点A，B在x轴的负半轴上，反比例函数y＝
（k1≠0）在第二象限内的图象经过正方形ABCD的顶点D（m，2）和BC边上的点G（n，
），直线y=k2x+b（k2≠0）经过点D，点G，则不等式≤k2x+b的解集为__________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】图1为含锐角是30°的直角三角尺，其边框为透明塑料制成（内、外直角三角形对应边互相平行且三处所示宽度相等）．将三角尺移向直径为4cm的⊙O，它的内Rt△ABC的斜边AB恰好等于⊙O的直径，它的外Rt△A′B′C′的直角边A′C′恰好与⊙O相切（如图2）．
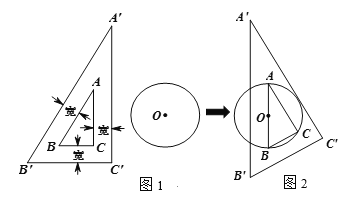
（1）求直角三角尺边框的宽；
（2）求边B′C′的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小明为探究函数
的图象和性质，需要画出函数图象，列表如下：
| …… |
|
|
|
|
|
|
|
|
|
| …… |
| …… |
|
|
|
|
|
|
|
|
|
| …… |
根据上表数据，在平面直角坐标系中描点，画出函数图象，如图如示，小明画出了图象的一部分．
（1）请你帮小明画出完整的的图象；
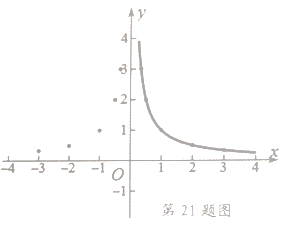
（2）观察函数图象，请写出这个函数的两条性质：
性质一： ；
性质二： ．
（3）利用上述图象，探究函数图象与直线
的关系；
①当
时， 直线与函数在第一象限的图象有一个交点
，则的坐标是 ；
②当
为何值时，讨论函数的图象与直线的交点个数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线
与
轴交于点
，与
轴交于点
（点
与点
不重合），抛物线
经过点
，抛物线的顶点为
．
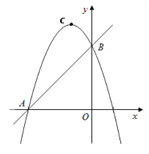
（1）
°；
（2）求
的值；
（3）在抛物线上是否存在点
，能够使
？如果存在，请求出点
的坐标；如果不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
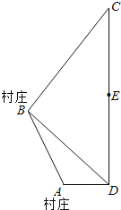
【题目】如图所示，A、B为两个村庄，AB、BC、CD为公路，BD为地，AD为河宽，且CD与AD互相垂直.现在要从E处开始铺设通往村庄A、村庄B的一电缆，共有如下两种铺设方案：
方案一：
； 方案二：
.
经测量得AB=4
千米，BC=10千米，CE=6千米，∠BDC＝45°，∠ABD＝15°．已知：地下电缆的修建费为2万元／千米，水下电缆的修建费为4万元／千米.
（1）求出河宽AD（结果保留根号）；
（2）求出公路CD的长；
（3）哪种方案铺设电缆的费用低？请说明你的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
