
【题目】如图所示,A、B为两个村庄,AB、BC、CD为公路,BD为地,AD为河宽,且CD与AD互相垂直.现在要从E处开始铺设通往村庄A、村庄B的一电缆,共有如下两种铺设方案:
方案一:![]() ; 方案二:
; 方案二:![]() .
.
经测量得AB=4![]() 千米,BC=10千米,CE=6千米,∠BDC=45°,∠ABD=15°.已知:地下电缆的修建费为2万元/千米,水下电缆的修建费为4万元/千米.
千米,BC=10千米,CE=6千米,∠BDC=45°,∠ABD=15°.已知:地下电缆的修建费为2万元/千米,水下电缆的修建费为4万元/千米.
(1)求出河宽AD(结果保留根号);
(2)求出公路CD的长;
(3)哪种方案铺设电缆的费用低?请说明你的理由.
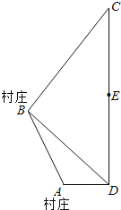
【答案】(1)6-2![]() 千米;(2)14千米;(3)方案一的铺设电缆费用低.
千米;(2)14千米;(3)方案一的铺设电缆费用低.
【解析】
(1)如图所示,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,由于
,由于![]() ,
,![]() ,故利用三角形外角等于不相邻两个内角和知
,故利用三角形外角等于不相邻两个内角和知![]() ,即在直角三角形中,知道斜边求邻边用余弦得
,即在直角三角形中,知道斜边求邻边用余弦得![]() (千米),又
(千米),又![]() (千米)
(千米)![]() ,所以可求出
,所以可求出![]() 的值;
的值;
(2)过点![]() 作
作![]() 于
于![]() 后,由矩形知
后,由矩形知![]() ,由勾股定理知
,由勾股定理知![]() 千米,有
千米,有![]() 千米;
千米;
(3)由(2)得![]() ,方案一的铺设费用为:
,方案一的铺设费用为:![]() 万元,方案二的铺设费用为:
万元,方案二的铺设费用为:![]() 万元.故方案一的铺设电缆费用低.
万元.故方案一的铺设电缆费用低.
(1)过点B作BF⊥AD,交DA的延长线于点F.
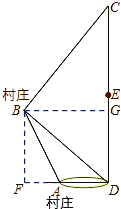
由题意得:∠BAF=∠ABD+∠ADB=15°+45°=60°,
在Rt△BFA中,
BF=ABsin60°=4![]() ×
×![]() =6(千米),
=6(千米),
AF=ABcos60°=4![]() ×
×![]() =2
=2![]() (千米).
(千米).
∵CD⊥AD,∠BDC=45°,
∴∠BDF=45°,
在Rt△BFD中,∵∠BDF=45°,
∴DF=BF=6千米.
∴AD=DF-AF=6-2![]() (千米).
(千米).
即河宽AD为(6-2![]() )千米;
)千米;
(2)过点B作BG⊥CD于G,易证四边形BFDG是正方形,
∴BG=BF=6千米.
在Rt△BGC中,CG=![]() =8(千米),
=8(千米),
∴CD=CG+GD=14千米.
即公路CD的长为14千米;
(3)方案一的铺设电缆费用低.
由(2)得DE=CD-CE=8千米.
∴方案一的铺设费用为:2(DE+AB)+4AD=40万元,
方案二的铺设费用为:2(CE+BC+AB)=(32+8![]() )万元.
)万元.
∵40<32+8![]() ,
,
∴方案一的铺设电缆费用低.


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:
【题目】在当前国际“新冠肺炎”疫情防控的紧要关头,“中国制造”呈现出强大实力.据国家海关总局统计,4月25日当天,中国的口罩出口量就达10.6亿只.将数10.6亿用科学记数法表示为m![]() 10n,那么m,n的值分别为()
10n,那么m,n的值分别为()
A.10.6,8B.10.6,9C.1.06,9D.1.06,10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 年
年![]() 月
月![]() 日下午,由
日下午,由![]() 名队员组成的扬州市第七批支援湖北医疗队,肩负着国家的重托和神圣职责使命启程出征,其中小李、小王和三个同事共五人直接派往一线某医院,根据该院人事安排需要先抽出一人去重症监护,再派两人到发热门诊,请你利用所学知识完成下列问题.
名队员组成的扬州市第七批支援湖北医疗队,肩负着国家的重托和神圣职责使命启程出征,其中小李、小王和三个同事共五人直接派往一线某医院,根据该院人事安排需要先抽出一人去重症监护,再派两人到发热门诊,请你利用所学知识完成下列问题.
(1)小李被派往重症监护的概率是 ;
(2)若正好抽出她们的一同事去往重症监护,请你利用画树状图或列表的方法,求出小李和小王同时被派往发热门诊的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明与小亮玩游戏,如图,两组相同的纸牌,每组三张,牌面数字分别是3,4,5.他们将卡片背面朝上,分组充分洗匀后,从每组纸牌中各摸出一张,称为一次游戏.当摸出的两张纸牌的牌面数字之和大于8,则小明获胜;当摸出的两张纸牌的牌面数字之和小于8,则小亮获胜.
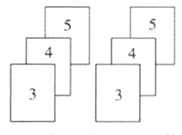
(1)请你用列表法或画树状图法求出小明获胜的概率;
(2)这个游戏公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
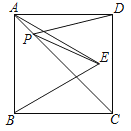
【题目】如图所示,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形内,在对角线AC上找到一点P,使PD+PE的和最小,则这个和的最小值是( )
A.![]() B.
B.![]() C.3D.
C.3D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
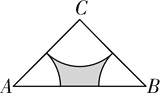
【题目】(2011贵州安顺)如图,在Rt△ABC中,∠C=90°,CA=CB=4,分别以A、B、C为圆心,以![]() AC为半径画弧,三条弧与边AB所围成的阴影部分的面积是 .
AC为半径画弧,三条弧与边AB所围成的阴影部分的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)发现探究:如图1,矩形![]() 和矩形
和矩形![]() 位似,
位似,![]() ,连接
,连接![]() ,则线段
,则线段![]() 与
与![]() 有何数量关系,关系是__________.直线
有何数量关系,关系是__________.直线![]() 与直线
与直线![]() 所夹锐角的度数是__________.
所夹锐角的度数是__________.
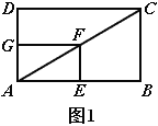
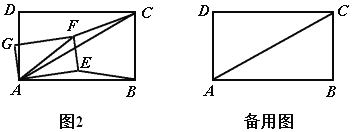
(2)拓展探究:如图2,将矩形![]() 绕点
绕点![]() 逆时针旋转角
逆时针旋转角![]()
![]() ,上面的结论是否仍然成立?如果成立,请就图2给出的情况加以证明.
,上面的结论是否仍然成立?如果成立,请就图2给出的情况加以证明.
(3)问题解决:若点![]() 是
是![]() 的中点,
的中点,![]() ,连接
,连接![]() ,
,![]() ,在矩形
,在矩形![]() 绕点
绕点![]() 旋转过程中,请直接写出
旋转过程中,请直接写出![]() 长的取值范围.
长的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,BC=3,动点P从B出发,以每秒1个单位的速度,沿射线BC方向移动,作△PAB关于直线PA的对称△PAB' ,设点P的运动时间为t(s).
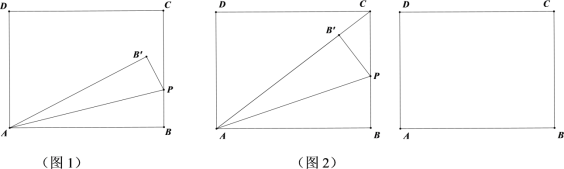
(1)若AB=2![]() .
.
①如图2,当点B' 落在AC上时,求t的值;
②是否存在异于图2的时刻,使得△PCB’是直角三角形?若存在,请直接写出所有符合题意的t值?若不存在,请说明理由.
(2)若四边形ABCD是正方形,直线PB'与直线CD相交于点M,当点P不与点C重合时,求证:∠PAM=45°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数![]() 的图象经过点(
的图象经过点(![]() ,
,![]() )和(
)和(![]() ,
,![]() ),完成下面问题:
),完成下面问题:
(1)求函数![]() 的表达式;
的表达式;
(2)在给出的平面直角坐标系中,请用适当的方法画出这个函数的图象,并写出这个函数的一条性质;

(3)已知函数![]() 的图象如图所示,结合你所画出
的图象如图所示,结合你所画出![]() 的图象,直接写出
的图象,直接写出![]() 的解集.
的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com