
����Ŀ����ͼ1���ھ���ABCD�У�BC=3������P��B��������ÿ��1����λ���ٶȣ�������BC�����ƶ�������PAB����ֱ��PA�ĶԳơ�PAB' �����P���˶�ʱ��Ϊt��s����
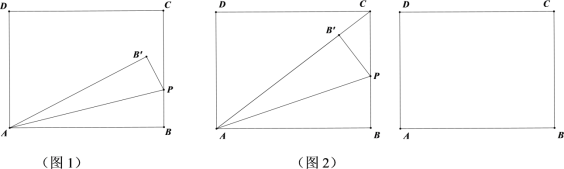
��1����AB=2![]() ��
��
����ͼ2������B' ����AC��ʱ����t��ֵ��
���Ƿ��������ͼ2��ʱ�̣�ʹ�á�PCB����ֱ�������Σ������ڣ���ֱ��д�����з��������tֵ���������ڣ���˵������.
��2�����ı���ABCD�������Σ�ֱ��PB'��ֱ��CD�ཻ�ڵ�M������P�����C�غ�ʱ����֤����PAM=45��.
���𰸡���1����t=2![]() ��4���ڴ��ڣ�t=2��t=6��t=2
��4���ڴ��ڣ�t=2��t=6��t=2![]() ����2���������
����2���������
��������
��1�������ù��ɶ������AC������PCB���ס�ACB���Ƴ�![]() ���ɽ�����⣮
���ɽ�����⣮
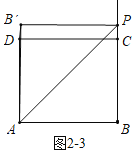
�ڷ��������ηֱ���⼴�ɣ���ͼ2-1�У�����PCB��=90��ʱ����ͼ2-2�У�����PCB��=90��ʱ����ͼ2-3�У�����CPB��=90��ʱ��
��2����ͼ3-1�У���t<3ʱ�����ı���ABCD�������Σ�֤����MDA�ա�MB��A�����ɵõ���������ͼ3-2�У���t>3ʱ�����APB=x������ȫ�������ε����ʣ����۲����Լ��ɽ�����⣮
�⣺��1������ͼ1�У�
���ı���ABCD�Ǿ��Σ�
���ABC=90���� ��![]()
�ߡ�PCB��=��ACB����PB��C=��ABC=90����
���PCB���ס�ACB��
��![]()
�� ![]()
��![]()
��![]()
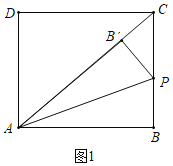
����ͼ2-1�У�����PCB��=90��ʱ��
���ı���ABCD�Ǿ��Σ� ���D=90����AB=CD=![]() AD=BC=3��
AD=BC=3��
��![]()
��![]()
��Rt��PCB������![]()
��![]()
��![]()
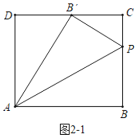
��ͼ2-2�У�����PCB��=90��ʱ��
��Rt��ADB����![]() ��
��
![]()
��Rt��PCB��������![]()
���t=6��
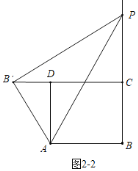
��ͼ2-3�У�����CPB��=90��ʱ����![]()
���ı���![]() Ϊ�����Σ�
������
![]()
![]()
��������������������t��ֵΪ2s��6s��![]() s��
s��
��2����ͼ3-1����t<3ʱ��
�֡߷��ۣ�
���1=��2��AB=AB������B=��AB��P
���ı���ABCD�������Σ�
��AD=AB=AB�� ����D=��B=��AB��P= 90��
��AM=AM
���MDA�ա�MB��A��HL��
���3=��4
���2+��3=45����
����PAM=45��
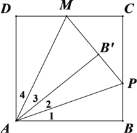
��������ͼ3-1��
��ͼ3-2����t>3ʱ�����APB=x
���PAB=90����x
���DAP��x
ͬ������MDA�ա�MB��A��HL��
���B��AM����DAM
�߷���
���PAB����PAB����90����x
���DAB������PAB������DAP��90����2x
���DAM��![]() ��DAB����45����x
��DAB����45����x
���MAP=��DAM+��PAD=45��
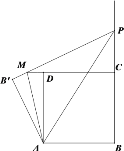
��ͼ3-2��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() ���
���![]() ���غϣ���������
���غϣ���������![]() ������
������![]() �������ߵĶ���Ϊ
�������ߵĶ���Ϊ![]() ��
��
��1��![]() ����
����
��2����![]() ��ֵ��
��ֵ��
��3�������������Ƿ���ڵ�![]() ���ܹ�ʹ
���ܹ�ʹ![]() ��������ڣ��������
��������ڣ��������![]() �����ꣻ��������ڣ���˵�����ɣ�
�����ꣻ��������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
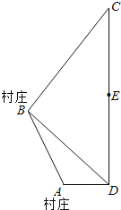
����Ŀ����ͼ��ʾ��A��BΪ������ׯ��AB��BC��CDΪ��·��BDΪ�أ�ADΪ�ӿ�����CD��AD���ഹֱ.����Ҫ��E����ʼ����ͨ����ׯA����ׯB��һ���£����������������跽����
����һ��![]() �� ��������
�� ��������![]() .
.
��������AB=4![]() ǧ�ף�BC=10ǧ�ף�CE=6ǧ�ף���BDC��45�㣬��ABD��15�㣮��֪�����µ��µ�����Ϊ2��Ԫ��ǧ�ף�ˮ�µ��µ�����Ϊ4��Ԫ��ǧ��.
ǧ�ף�BC=10ǧ�ף�CE=6ǧ�ף���BDC��45�㣬��ABD��15�㣮��֪�����µ��µ�����Ϊ2��Ԫ��ǧ�ף�ˮ�µ��µ�����Ϊ4��Ԫ��ǧ��.
��1������ӿ�AD������������ţ���
��2�������·CD�ij���
��3�����ַ���������µķ��õͣ���˵���������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
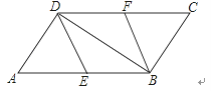
����Ŀ����ͼ����ABCD�У�E��F�ֱ�Ϊ��AB��CD���е㣬����DE��BF��BD��
(1)��֤����ADE�ա�CBF
(2)��AD��BDʱ�������ж��ı���BFDE����״����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʦΪ�˽����ν̵��������ѧ����ѧѧϰ���������ѧ������һ�β��ԣ������������ijɼ����ٷ��ƣ����������ݣ��ɼ������������������ͷ�������������˲�����Ϣ��
��A��B����ѧ�����������������ͬ����ѧ�ɼ���������Ƶ���ֲ�ֱ��ͼ���£����ݷֳ�5�飺x<60��60��x<70��70��x<80��80��x<90��90��x��100����
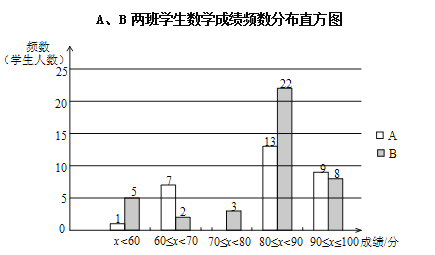
��A��B����ѧ�����Գɼ���80��x<90��һ����������£�
A�ࣺ80 80 82 83 85 85 86 87 87 87 88 89 89
B�ࣺ80 80 81 81 82 82 83 84 84 85 85 86 86 86 87 87 87 87 87 88 88 89
��A��B����ѧ�����Գɼ���ƽ��������λ�����������£�
ƽ���� | ��λ�� | ���� | |
A�� | 80.6 | m | 96.9 |
B�� | 80.8 | n | 153.3 |
����������Ϣ���ش��������⣺
��1����ȫ��ѧ�ɼ�Ƶ���ֲ�ֱ��ͼ��
��2��д������m��n��ֵ��
��3������Աȷ���A��B����ѧ������ѧѧϰ��������ٴ�������ͬ�ĽǶȷ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ�˽�ѧ���İ�ȫ��ʶ�������ȫУ��Χ�������ȡ����ѧ�������ʾ����飬���ݵ���������ѧ���İ�ȫ��ʶ�ֳ�������������һ����������ǿ��������ǿ���ĸ���Σ������Ƴ����������в�������ͳ��ͼ��

����������Ϣ������������⣺
��1����ε���һ����ȡ�� ��ѧ�������а�ȫ��ʶΪ����ǿ����ѧ��ռ������ѧ�������İٷֱ��� ��
��2���뽫����ͳ��ͼ����������
��3����У��1800��ѧ������Ҫ��ȫ��ʶΪ������������һ������ѧ��ǿ����ȫ���������ݵ�����������ȫУ��Ҫǿ����ȫ������ѧ��Լ�� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
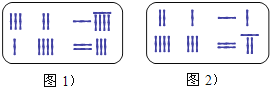
����Ŀ�����������������ҹ���������ඩ��һ����ѧ���������������ġ����̡�һ���һ�η�����������ﲼ�ö��ɵģ��������������е����ͼ�����ŵģ�Ϊ��ͼ���㣬���ǰ�����Ϊ���ţ���ͼ1��ͼ2��ͼ�и��д������г���������ֱ��ʾδ֪��x��y��ϵ������Ӧ�ij������ͼ1��ʾ�����ͼ��������������Ϥ�ķ�������ʽ��������������![]() �����Ƶأ�ͼ2��ʾ�����ͼ���ǿ��Ա���Ϊ��������
�����Ƶأ�ͼ2��ʾ�����ͼ���ǿ��Ա���Ϊ��������
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������龳
���ۺ�ʵ�����ϣ�ͬѧ�����������κ�ֱ�ߵ���ת��Ϊ������鿪չ��ѧ̽�������֪������ABCD��ֱ��PQ������A�����Ƶ�A��ת������B����ֱ��PQ�ĶԳƵ�E��ֱ��DE��ֱ��PQ�ڵ�F������AE��BE��

��������
��1����ͼ1�����PAB=25�����ADF=�� ������
��2��������С�顱��ͬѧ�Ƿ��֣���BEF�Ķ�����һ����ֵ�����ֵΪ�� ����
��3��������С�顱��ͬѧ�Ƿ��֣��߶�AB��DF��EF֮����������������ϵ����д����һ��ϵʽ����˵�����ɣ�
��չӦ��
��4����ͼ2����ֱ��PQ��������ABCD���ⲿʱ������ȡС������ͬѧ�Ƿ��֣�3���Ľ�����Ȼ����������������⣻��DF=3![]() ��EF=4
��EF=4![]() ��ֱ��д��������ABCD�ı߳���
��ֱ��д��������ABCD�ı߳���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
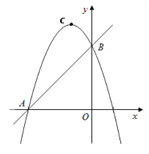
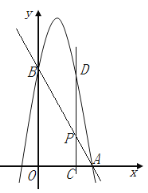
����Ŀ����ͼ����ֱ֪��y=��2x+4�ֱ�x�ᡢy���ڵ�A��B�������߹�A��B���㣬������y=��2x2+bx+c��A��B���㣮
��1���������ߵĽ���ʽ��
��2����ͼ1����P���߶�AB��һ���㣬����P��PC��x���ڵ�C�����������ڵ�D�����䶥��ΪM����Գ��ύAB�ڵ�N���Ƿ���ڵ�P��ʹ�ı���MNPDΪ���Σ���˵�����ɣ�
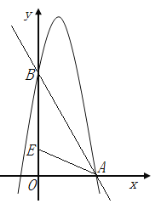
��3����ͼ2����E��0��1����y���ϣ�����AE�����������Ƿ����һ��F��ʹ��FEO���EAO�����������ڣ����F�ĺ����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com