
【题目】如图,已知直线y=﹣2x+4分别交x轴、y轴于点A、B,抛物线过A,B两点,抛物线y=﹣2x2+bx+c过A、B两点.
(1)求抛物线的解析式;
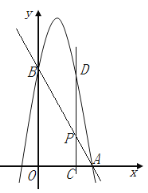
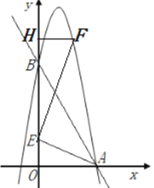
(2)如图1,点P是线段AB上一动点,过点P作PC⊥x轴于点C,交抛物线于点D,设其顶点为M,其对称轴交AB于点N.是否存在点P,使四边形MNPD为菱形?并说明理由;
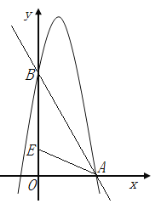
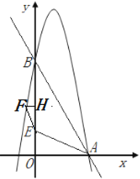
(3)如图2,点E(0,1)在y轴上,连接AE,抛物线上是否存在一点F,使∠FEO与∠EAO互补,若存在,求点F的横坐标;若不存在,请说明理由.
【答案】(1)y=﹣2x2+2x+4;(2)不存在点P,使四边形MNPD为菱形;理由见解析;(3)存在,点F的横坐标为![]() 或
或![]() 时,∠FEO与∠EAO互补.
时,∠FEO与∠EAO互补.
【解析】
(1)求出直线y=﹣2x+4与x轴、y轴交点A、B的坐标,再利用待定系数法求解即可;
(2)利用函数解析式求出抛物线的顶点M的坐标为(![]() ,
,![]() ),求出MN的长度,
),求出MN的长度,
设P点坐标为(m,﹣2m+4),则D(m,﹣2m2+2m+4),求出PD=﹣2m2+2m+4﹣(﹣2m+4)=﹣2m2+4m,根据平行四边形的性质列PD=MN求出m,得到PN=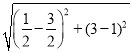 =
=![]() ,由PN≠MN确定不存在满足条件的点P;
,由PN≠MN确定不存在满足条件的点P;
(3)过点F作FH⊥y轴于点H,则∠FEO+∠FEH=180°,当∠FEO+∠EAO=180°时,推出∠FEH=∠EAO,证明△AOE∽△∠EFH,得到![]() ,再分两种情况:当点F在y轴右侧时,点F在y轴左侧时,分别将线段长度代入比例式求出t即可.
,再分两种情况:当点F在y轴右侧时,点F在y轴左侧时,分别将线段长度代入比例式求出t即可.
解:(1)当x=0时,y=4,当y=0时,x=2,
∴点A(2,0),点B(0,4),
把A(2,0),B(0,4)分别代入y=﹣2x2+bx+c中得
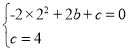 ,
,
解之得![]() ,
,
∴抛物线解析式为:y=﹣2x2+2x+4;
(2)不存在.
理由如下:y=﹣2x2+2x+4=![]() (x-
(x-![]() )2+
)2+![]() ,
,
∴抛物线顶点M(![]() ,
,![]() ),
),
当x=![]() 时,y=
时,y=![]() =-3,
=-3,
∴MN=![]() ﹣3=
﹣3=![]() ,
,
设P点坐标为(m,﹣2m+4),则D(m,﹣2m2+2m+4),
∴PD=﹣2m2+2m+4﹣(﹣2m+4)=﹣2m2+4m,
∵PD∥MN,
当PD=MN时,四边形MNPD为平行四边形,即﹣2m2+4m=![]() ,
,
解得m1=![]() (舍去),m2=
(舍去),m2=![]() ,此时P点坐标为(
,此时P点坐标为(![]() ,1),
,1),
∵PN=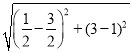 =
=![]() ,
,
∴PN≠MN,
∴平行四边形MNPD不为菱形,
∴不存在点P,使四边形MNPD为菱形;
(3)存在.
如图,过点F作FH⊥y轴于点H,则∠FEO+∠FEH=180°,
当∠FEO+∠EAO=180°时,∠FEH=∠EAO,
∵∠FHE=∠AOE=90°,
∴△AOE∽△∠EFH,
∴![]() ,
,
设点F(t,﹣2t2+2t+4),则HE=﹣2t2+2t+4﹣1=﹣2t2+2t+3,
当点F在y轴右侧时,HF=t,
∴![]() ,
,
解之得:t=![]() ,
,
∵点F在y轴右侧,
∴t=![]() ,
,
当点F在y轴左侧时,BF=-t,
∴![]() ,
,
解之得:t=![]() ,
,
∵点F在y轴左侧
∴t=![]() .
.
综上所述:当点F的横坐标为![]() 或
或![]() 时,∠FEO与∠EAO互补.
时,∠FEO与∠EAO互补.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
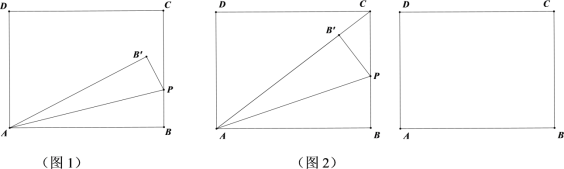
【题目】如图1,在矩形ABCD中,BC=3,动点P从B出发,以每秒1个单位的速度,沿射线BC方向移动,作△PAB关于直线PA的对称△PAB' ,设点P的运动时间为t(s).
(1)若AB=2![]() .
.
①如图2,当点B' 落在AC上时,求t的值;
②是否存在异于图2的时刻,使得△PCB’是直角三角形?若存在,请直接写出所有符合题意的t值?若不存在,请说明理由.
(2)若四边形ABCD是正方形,直线PB'与直线CD相交于点M,当点P不与点C重合时,求证:∠PAM=45°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数![]() 的图象经过点(
的图象经过点(![]() ,
,![]() )和(
)和(![]() ,
,![]() ),完成下面问题:
),完成下面问题:
(1)求函数![]() 的表达式;
的表达式;
(2)在给出的平面直角坐标系中,请用适当的方法画出这个函数的图象,并写出这个函数的一条性质;

(3)已知函数![]() 的图象如图所示,结合你所画出
的图象如图所示,结合你所画出![]() 的图象,直接写出
的图象,直接写出![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小学学生较多,为了便于学生尽快就餐,师生约定:早餐一人一份,一份两样,一样一个,食堂师傅在窗口随机发放(发放的食品价格一样),食堂在某天早餐提供了猪肉包、面包、鸡蛋、油饼四样食品.
(1)按约定,“小李同学在该天早餐得到两个油饼”是 事件;(可能,必然,不可能)
(2)请用列表或树状图的方法,求出小张同学该天早餐刚好得到猪肉包和油饼的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
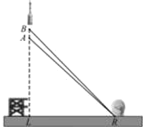
【题目】北京时间2020年5月12日9时16分,我国自主研制的快舟一号甲运载火箭在酒泉卫星发射中心发射成功.此次发射的“行云二号”01星命名为“行云·武汉号”,并通过在火箭箭体上涂刷“英雄武汉伟大中国”和“致敬医护工作者群像”的方式,致敬武汉、武汉人民和广大医护工作者.如图,火箭从地面L处发射,当火箭达到A点时,从位于地面R处雷达站测得AR的距离是6km,仰角为42.4°;1秒后火箭到达B点,此时测得仰角为45.5°求这枚火箭从A到B的平均速度是多少(结果精确到0.01)?(参考数据:sin42.4°≈0.67,cos42.4°≈0.74,tan42.4°≈0.905,sin45.5°≈0.71,cos45.5°≈0.70,tan45.5°≈1.02)
查看答案和解析>>
科目:初中数学 来源: 题型:
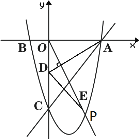
【题目】如图,抛物线![]() 经过点A(3,0),B(
经过点A(3,0),B(![]() ,0),与y轴交于点C,点P是抛物线在第四象限内的一点.
,0),与y轴交于点C,点P是抛物线在第四象限内的一点.
(1)求抛物线解析式;
(2)点D是线段OC的中点,OP⊥AD,点E是射线OP上一点,OE=AD,求DE的长;
(3)连接CP,AP,是否存在点P,使得OP平分四边形ABCP的面积?若存在,求点P的坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某软件开发公司开发了A、B两种软件,每种软件成本均为1400元,售价分别为2000元、1800元,这两种软件每天的销售额共为112000元,总利润为28000元.
(1)该店每天销售这两种软件共多少个?
(2)根据市场行情,公司拟对A种软件降价销售,同时提高B种软件价格.此时发现,A种软件每降50元可多卖1件,B种软件每提高50元就少卖1件.如果这两种软件每天销售总件数不变,那么这两种软件一天的总利润最多是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
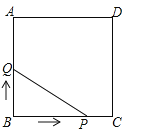
【题目】(3分)如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )
A.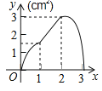 B.
B.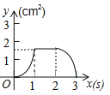 C.
C.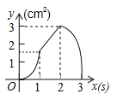 D.
D.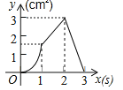
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了做好“营造清洁生活环境”活动的宣传,对本校学生进行了有关知识的测试,测试后随机抽取了部分学生的测试成绩,按“优秀、良好、及格、不及格”四个等级进行统计分析,并将分析结果绘制成如下两幅不完整的统计图:
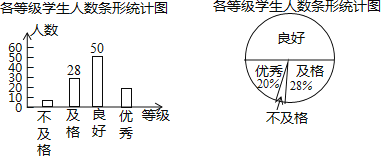
(1)求抽取的学生总人数;
(2)抽取的学生中,等级为“优秀”的人数为 人;扇形统计图中等级为“不合格”部分的圆心角的度数为 °;
(3)补全条形统计图;
(4)若该校有学生3500人,请根据以上统计结果估计成绩等级为“优秀”和“良好”的学生共有多少人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com