
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC,BC于点D,E,点F在AC的延长线上,且∠BAC=2∠CBF.
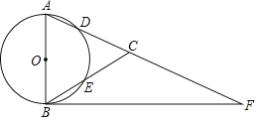
(1)求证:BF是⊙O的切线;
(2)若⊙O的直径为3,sin∠CBF=![]() ,求BC长.
,求BC长.
【答案】(1)见解析;(2)![]()
【解析】
(1)连接AE,利用直径所对的圆周角是直角,从而判定直角三角形,利用直角三角形两锐角相等得到直角,从而证明∠ABF=90°.
(2)解直角三角形即可得到结论.
解:(1)证明:连接AE,
∵AB是⊙O的直径,
∴∠AEB=90°,
∴∠1+∠2=90°.
∵AB=AC,
∴2∠1=∠CAB.
∵∠BAC=2∠CBF,
∴∠1=∠CBF
∴∠CBF+∠2=90°
即∠ABF=90°
∵AB是⊙O的直径,
∴直线BF是⊙O的切线;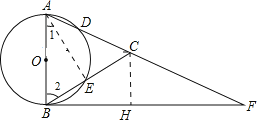
(2)解:过点C作CH⊥BF于H.
∵sin∠CBF=![]() ,∠1=∠CBF,
,∠1=∠CBF,
∴sin∠1=![]() ,
,
∵在Rt△AEB中,∠AEB=90°,AB=3,
∴BE=ABsin∠1=3×![]() =
=![]() ,
,
∵AB=AC,∠AEB=90°,
∴BC=2BE=![]() .
.


科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 经过点
经过点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
![]() 求这条抛物线的解析式;
求这条抛物线的解析式;
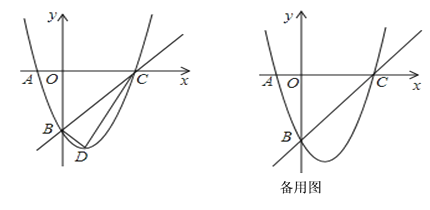
![]() 如图1,点P是第三象限内抛物线上的一个动点,当四边形
如图1,点P是第三象限内抛物线上的一个动点,当四边形![]() 的面积最大时,求点
的面积最大时,求点![]() 的坐标;
的坐标;
![]() 如图2,线段
如图2,线段![]() 的垂直平分线交
的垂直平分线交![]() 轴于点
轴于点![]() ,垂足为
,垂足为![]() 为抛物线的顶点,在直线
为抛物线的顶点,在直线![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 的周长最小?若存在,求出点
的周长最小?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,![]() 是一元二次方程
是一元二次方程![]() 的两个实数根,且
的两个实数根,且![]() ,抛物线
,抛物线![]() 的图象经过点
的图象经过点![]() ,
,![]() ,如图所示.
,如图所示.
(1)求这个抛物线的解析式;
(2)设(1)中的抛物线与![]() 轴的另一个交点为
轴的另一个交点为![]() ,抛物线的顶点为
,抛物线的顶点为![]() ,试求出点
,试求出点![]() ,
,![]() 的坐标,并判断
的坐标,并判断![]() 的形状;
的形状;
(3)点![]() 是直线
是直线![]() 上的一个动点(点
上的一个动点(点![]() 不与点
不与点![]() 和点
和点![]() 重合),过点
重合),过点![]() 作
作![]() 轴的垂线,交抛物线于点
轴的垂线,交抛物线于点![]() ,点
,点![]() 在直线
在直线![]() 上,距离点
上,距离点![]() 为
为![]() 个单位长度,设点
个单位长度,设点![]() 的横坐标为
的横坐标为![]() ,
,![]() 的面积为
的面积为![]() ,求出
,求出![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图,已知抛物线![]() 与直线AB相交于A(﹣3,0),B(0,3)两点.
与直线AB相交于A(﹣3,0),B(0,3)两点.
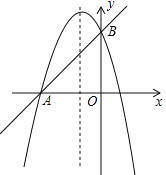
(1)求这条抛物线的解析式;
(2)设C是抛物线对称轴上的一动点,求使∠CBA=90°的点C的坐标;
(3)探究在抛物线上是否存在点P,使得△APB的面积等于3?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() 点
点![]() 在边
在边![]() 上(点
上(点![]() 与点
与点![]() 不重合),以点
不重合),以点![]() 为圆心,
为圆心,![]() 为半径作⊙
为半径作⊙![]() 交边
交边![]() 于另一点
于另一点![]() ,
,![]() ,交边
,交边![]() 于点
于点![]() .
.
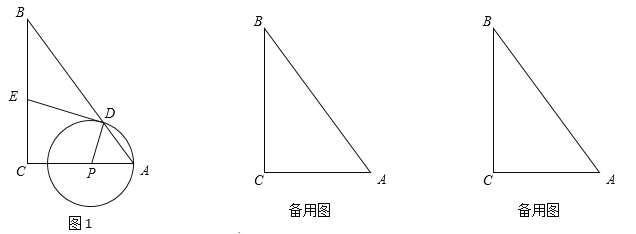
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() 关于
关于![]() 的函数关系式并写出定义域;
的函数关系式并写出定义域;
(3)延长![]() 交
交![]() 的延长线于点
的延长线于点![]() ,联结
,联结![]() ,若
,若![]() 与
与![]() 相似,求线段
相似,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解我市某中学“书香校园”的建设情况,在该校随机抽取了50名学生,调查了解他们一周阅读课外书籍的时间,并将调查结果绘制成如图所示的频数分布直方图(每小组的时间包含最小值,不包含最大值),根据图中信息估计该校1500名学生中,一周课外阅读时间不少于4小时的人数约为( )

A.300B.600C.900D.1200
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在当前国际“新冠肺炎”疫情防控的紧要关头,“中国制造”呈现出强大实力.据国家海关总局统计,4月25日当天,中国的口罩出口量就达10.6亿只.将数10.6亿用科学记数法表示为m![]() 10n,那么m,n的值分别为()
10n,那么m,n的值分别为()
A.10.6,8B.10.6,9C.1.06,9D.1.06,10
查看答案和解析>>
科目:初中数学 来源: 题型:
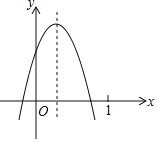
【题目】已知二次函数 y=ax2+bx+c (a≠0)的图象如图所示,则下列结论:①abc<0;②b2﹣4ac<0;③2a+b>0;④a﹣b+c<0,其中正确的个数( )
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明与小亮玩游戏,如图,两组相同的纸牌,每组三张,牌面数字分别是3,4,5.他们将卡片背面朝上,分组充分洗匀后,从每组纸牌中各摸出一张,称为一次游戏.当摸出的两张纸牌的牌面数字之和大于8,则小明获胜;当摸出的两张纸牌的牌面数字之和小于8,则小亮获胜.
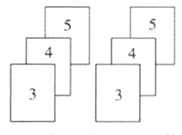
(1)请你用列表法或画树状图法求出小明获胜的概率;
(2)这个游戏公平吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com