
【题目】图1为含锐角是30°的直角三角尺,其边框为透明塑料制成(内、外直角三角形对应边互相平行且三处所示宽度相等).将三角尺移向直径为4cm的⊙O,它的内Rt△ABC的斜边AB恰好等于⊙O的直径,它的外Rt△A′B′C′的直角边A′C′恰好与⊙O相切(如图2).
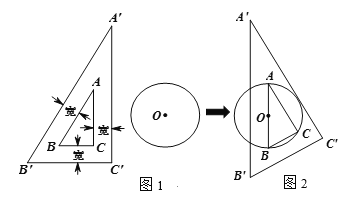
(1)求直角三角尺边框的宽;
(2)求边B′C′的长.
【答案】(1)1cm;(2)![]() +3
+3
【解析】
(1)过O作OD⊥A′C′于D,交AC于E,由AC与A′C′,根据与平行线中的一条直线垂直,与另一条也垂直,得到OD与AC垂直,可得DE为三角尺的宽, 由A′C′与圆O相切,根据切线的性质得到OD为圆的半径,根据直径AB的长,求出半径OA,OB及OD的长,在直角三角形AOE中,根据∠A=30°,利用直角三角形中,30°角所对的直角边等于斜边的一半可得出OE等于OA的一半,由OA的长求出OE的长,再由OD﹣OE求出DE的长,即三角尺的宽为1;
(2)设直线AC交A′B′于M,交B′C′于N,过A点作AH⊥A′B′于H,则有∠AMH=30°,AH=1,得到AM=2AH=2,可计算出MN,在Rt△MB′N中利用含30°的直角三角形三边的关系得到B′N长,即可得出答案.
解:(1)过O作OD⊥A′C′于D,交AC于E,
∵AC∥A′C′,
∴AC⊥OD,
∵A′C′与⊙O相切,AB为圆O的直径,且AB=4cm,
∴OD=OA=OB=![]() AB=
AB=![]() ×4=2(cm),
×4=2(cm),
在Rt△AOE中,∠A=30°,
∴OE=![]() OA=
OA=![]() ×2=1(cm),
×2=1(cm),
∴DE=OD-OE=2-1=1(cm)
则三角尺的宽为1cm;
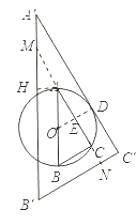
(2)设直线AC交A′B′于M,交B′C′于N,过A点作AH⊥A′B′于H,
则有∠AMH=30°,AH=1,
得到AM=2AH=2,
∴MN=AM+AC+CN=3+2![]() ,
,
∵在Rt△MB′N中,∠B′MN=30°,
∴B′N=MN×tan30°=(3+2![]() )×
)×![]() =(
=(![]() +2)cm,
+2)cm,
则B′C′=B′N+NC′=![]() +3.
+3.
∴B′C′=3+![]() .
.


科目:初中数学 来源: 题型:
【题目】(阅读理解)
我们将使得函数值为零的自变量的值称为函数的零点值,此时的点称为函数的零点.例如,对于函数y=x-1,令y=0,可得x=1,我们就说1是函数y=x-1的零点值,点(1,0)是函数y=x-1的零点.
(问题解决)
(1)已知函数![]() ,则它的零点坐标为________;
,则它的零点坐标为________;
(2)若二次函数y=x2-2x+m有两个零点,则实数m的取值范围是________;
(3)已知二次函数![]() 的两个零点都是整数点,求整数k的值.
的两个零点都是整数点,求整数k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图,已知抛物线![]() 与直线AB相交于A(﹣3,0),B(0,3)两点.
与直线AB相交于A(﹣3,0),B(0,3)两点.
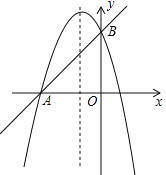
(1)求这条抛物线的解析式;
(2)设C是抛物线对称轴上的一动点,求使∠CBA=90°的点C的坐标;
(3)探究在抛物线上是否存在点P,使得△APB的面积等于3?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解我市某中学“书香校园”的建设情况,在该校随机抽取了50名学生,调查了解他们一周阅读课外书籍的时间,并将调查结果绘制成如图所示的频数分布直方图(每小组的时间包含最小值,不包含最大值),根据图中信息估计该校1500名学生中,一周课外阅读时间不少于4小时的人数约为( )

A.300B.600C.900D.1200
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在当前国际“新冠肺炎”疫情防控的紧要关头,“中国制造”呈现出强大实力.据国家海关总局统计,4月25日当天,中国的口罩出口量就达10.6亿只.将数10.6亿用科学记数法表示为m![]() 10n,那么m,n的值分别为()
10n,那么m,n的值分别为()
A.10.6,8B.10.6,9C.1.06,9D.1.06,10
查看答案和解析>>
科目:初中数学 来源: 题型:
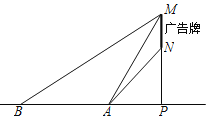
【题目】某数学社团成员想利用所学的知识测量某广告牌的宽度![]() 图中线段MN的长
图中线段MN的长![]() ,直线MN垂直于地面,垂足为点
,直线MN垂直于地面,垂足为点![]() 在地面A处测得点M的仰角为
在地面A处测得点M的仰角为![]() 、点N的仰角为
、点N的仰角为![]() ,在B处测得点M的仰角为
,在B处测得点M的仰角为![]() ,
,![]() 米,且A、B、P三点在一直线上
米,且A、B、P三点在一直线上![]() 请根据以上数据求广告牌的宽MN的长.
请根据以上数据求广告牌的宽MN的长.
![]() 参考数据:
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数 y=ax2+bx+c (a≠0)的图象如图所示,则下列结论:①abc<0;②b2﹣4ac<0;③2a+b>0;④a﹣b+c<0,其中正确的个数( )
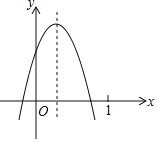
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形的周长为60.
(1)当该矩形的面积为200时,求它的边长;
(2)请表示出这个矩形的面积与其一边长的关系,并求出当矩形面积取得最大值时,矩形的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2011贵州安顺)如图,在Rt△ABC中,∠C=90°,CA=CB=4,分别以A、B、C为圆心,以![]() AC为半径画弧,三条弧与边AB所围成的阴影部分的面积是 .
AC为半径画弧,三条弧与边AB所围成的阴影部分的面积是 .
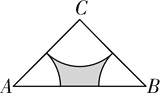
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com